Structure and Interpretation of Computer Programs (24 page)

(define (sum-odd-squares tree)
  (cond ((null? tree) 0)  
        ((not (pair? tree))
         (if (odd? tree) (square tree) 0))
        (else (+ (sum-odd-squares (car tree))
                 (sum-odd-squares (cdr tree))))))

On the surface, this procedure is very different from the following
one, which constructs a list of all the even Fibonacci numbers
F
i
b
(
k
), where
k
is less than or equal to a given integer
n
:

(define (even-fibs n)
  (define (next k)
    (if (> k n)
        nil
        (let ((f (fib k)))
          (if (even? f)
              (cons f (next (+ k 1)))
              (next (+ k 1))))))
  (next 0))

Despite the fact that these two procedures are structurally very
different, a more abstract description of the two computations reveals
a great deal of similarity. The first program

• enumerates the leaves of a tree;
  
• filters them, selecting the odd ones;
  
• squares each of the selected ones; and
  
• accumulates the results using
  +
  , starting with 0.
  

The second program

• enumerates the integers from 0 to
  n
  ;
  
• computes the Fibonacci number for each integer;
  
• filters them, selecting the even ones; and
  
• accumulates the results using
  cons
  , starting with the
  empty list.
  

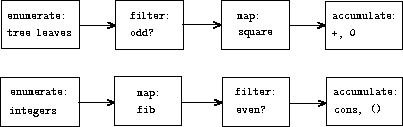
A signal-processing engineer would find it natural to conceptualize
these processes in terms of signals flowing through a cascade of
stages, each of which implements part of the program plan, as shown in
figure 
2.7
. In
sum-odd-squares
, we
begin with an
enumerator
, which generates a “signal”
consisting of the leaves of a given tree. This signal is passed
through a
filter
, which eliminates all but the odd elements.
The resulting signal is in turn passed through a
map
, which is a
“transducer” that applies the
square
procedure to each
element. The output of the map is then fed to an
accumulator
,
which combines the elements using
+
, starting from an initial 0.
The plan for
even-fibs
is analogous.

Figure 2.7:
  The signal-flow plans for the procedures
sum-odd-squares
(top) and
even-fibs
(bottom) reveal the
commonality between the two programs.

Unfortunately, the two procedure definitions above fail to exhibit this
signal-flow structure. For instance, if we examine the
sum-odd-squares
procedure, we find that the enumeration is
implemented partly by the
null?
and
pair?
tests and partly
by the tree-recursive structure of the procedure. Similarly, the
accumulation is found partly in the tests and partly in the addition used
in the recursion. In general, there are no distinct parts of either
procedure that correspond to the elements in the signal-flow
description.
Our two procedures decompose the computations in a different way,
spreading the enumeration over the program and mingling it with the
map, the filter, and the accumulation. If we could organize our
programs to make the signal-flow structure manifest in the procedures
we write, this would increase the conceptual clarity of the resulting
code.

The key to organizing programs so as to more clearly reflect the
signal-flow structure is to concentrate on the “signals” that flow
from one stage in the process to the next. If we represent these
signals as lists, then we can use list operations to implement the
processing at each of the stages. For instance, we can implement the
mapping stages of the signal-flow diagrams using the
map
procedure from section 
2.2.1
:

(map square (list 1 2 3 4 5))
(1 4 9 16 25)

Filtering a sequence to select only those elements that satisfy a
given predicate is accomplished by

(define (filter predicate sequence)
  (cond ((null? sequence) nil)
        ((predicate (car sequence))
         (cons (car sequence)
               (filter predicate (cdr sequence))))
        (else (filter predicate (cdr sequence)))))

For example,

(filter odd? (list 1 2 3 4 5))
(1 3 5)

Accumulations can be implemented by

(define (accumulate op initial sequence)
  (if (null? sequence)
      initial
      (op (car sequence)
          (accumulate op initial (cdr sequence)))))
(accumulate + 0 (list 1 2 3 4 5))
15
(accumulate * 1 (list 1 2 3 4 5))
120
(accumulate cons nil (list 1 2 3 4 5))
(1 2 3 4 5)

All that remains to implement signal-flow diagrams is to enumerate the
sequence of elements to be processed. For
even-fibs
, we need to
generate the sequence of
integers in a given range, which we can do as follows:

(define (enumerate-interval low high)
  (if (> low high)
      nil
      (cons low (enumerate-interval (+ low 1) high))))
(enumerate-interval 2 7)
(2 3 4 5 6 7)

To enumerate the leaves of a tree, we can use
¹⁴

(define (enumerate-tree tree)
  (cond ((null? tree) nil)
        ((not (pair? tree)) (list tree))
        (else (append (enumerate-tree (car tree))
                      (enumerate-tree (cdr tree))))))
(enumerate-tree (list 1 (list 2 (list 3 4)) 5))
(1 2 3 4 5)

Now we can reformulate
sum-odd-squares
and
even-fibs
as in
the signal-flow diagrams. For
sum-odd-squares
, we enumerate the
sequence of leaves of the tree, filter this to keep only the odd
numbers in the sequence, square each element, and sum the results:

(define (sum-odd-squares tree)
  (accumulate +
              0
              (map square
                   (filter odd?
                           (enumerate-tree tree)))))

For
even-fibs
, we enumerate the integers from 0 to
n
, generate
the Fibonacci number for each of these integers, filter the resulting
sequence to keep only the even elements, and accumulate the results
into a list:

(define (even-fibs n)
  (accumulate cons
              nil
              (filter even?
                      (map fib
                           (enumerate-interval 0 n)))))

The value of expressing programs as sequence operations is that this
helps us make program designs that are modular, that is, designs that
are constructed by combining relatively independent pieces. We can
encourage modular design by providing a library of standard components
together with a conventional interface for connecting the components
in flexible ways.

Modular construction is a powerful strategy for
controlling complexity in engineering design. In real
signal-processing applications, for example, designers regularly build
systems by cascading elements selected from standardized families of
filters and transducers. Similarly, sequence operations provide a
library of standard program elements that we can mix and match. For
instance, we can reuse pieces from the
sum-odd-squares
and
even-fibs
procedures in a program that constructs a list of the
squares of the first
n
+ 1 Fibonacci numbers:

(define (list-fib-squares n)
  (accumulate cons
              nil
              (map square
                   (map fib
                        (enumerate-interval 0 n)))))
(list-fib-squares 10)
(0 1 1 4 9 25 64 169 441 1156 3025)

We can rearrange the pieces and use them in computing the product of
the odd integers in a sequence:

(define (product-of-squares-of-odd-elements sequence)
  (accumulate *
              1
              (map square
                   (filter odd? sequence))))
(product-of-squares-of-odd-elements (list 1 2 3 4 5))
225

We can also formulate conventional data-processing applications in
terms of sequence operations. Suppose we have a sequence of personnel
records and we want to find the salary of the highest-paid programmer.
Assume that we have a selector
salary
that returns the salary of
a record, and a predicate
programmer?
that tests if a record is
for a programmer. Then we can write

(define (salary-of-highest-paid-programmer records)
  (accumulate max
              0
              (map salary
                   (filter programmer? records))))

These examples give just a hint of the vast range of operations that
can be expressed as sequence operations.
¹⁵

Sequences, implemented here as lists, serve
as a conventional interface that permits us to combine processing
modules. Additionally, when we uniformly represent structures as
sequences, we have localized the data-structure dependencies in our
programs to a small number of sequence operations. By changing these,
we can experiment with alternative representations of sequences, while
leaving the overall design of our programs intact. We will exploit
this capability in section 
3.5
, when we generalize the
sequence-processing paradigm to admit infinite sequences.

Exercise 2.33.
  Fill in the missing expressions to complete the following definitions
of some basic list-manipulation operations as accumulations:

(define (map p sequence)
  (accumulate (lambda (x y) <
??
>) nil sequence))
(define (append seq1 seq2)
  (accumulate cons <
??
> <
??
>))
(define (length sequence)
  (accumulate <
??
> 0 sequence))

Exercise 2.34.
  
Evaluating a polynomial in
x
at a given value of
x
can be
formulated as an accumulation. We evaluate the polynomial

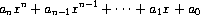
using a well-known algorithm called
Horner's rule
, which
structures the computation as

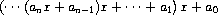
In other words, we start with
a
_n
, multiply by
x
, add
a
_n
-1
,
multiply by
x
, and so on, until we reach
a
₀
.
¹⁶
Fill in the following template to produce a procedure that evaluates a
polynomial using Horner's rule.
Assume that the coefficients of the
polynomial are arranged in a sequence, from
a
₀
through
a
_n
.

(define (horner-eval x coefficient-sequence)
  (accumulate (lambda (this-coeff higher-terms) <
??
>)
              0
              coefficient-sequence))