Structure and Interpretation of Computer Programs (19 page)

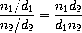
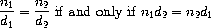
We can express these rules as procedures:

(define (add-rat x y)
  (make-rat (+ (* (numer x) (denom y))
               (* (numer y) (denom x)))
            (* (denom x) (denom y))))
(define (sub-rat x y)
  (make-rat (- (* (numer x) (denom y))
               (* (numer y) (denom x)))
            (* (denom x) (denom y))))
(define (mul-rat x y)
  (make-rat (* (numer x) (numer y))
            (* (denom x) (denom y))))
(define (div-rat x y)
  (make-rat (* (numer x) (denom y))
            (* (denom x) (numer y))))
(define (equal-rat? x y)
  (= (* (numer x) (denom y))
     (* (numer y) (denom x))))

Now we have the operations on rational numbers defined in terms of the
selector and constructor procedures
numer
,
denom
, and
make-rat
.
But we haven't yet defined these.
What we need is some way to glue together a numerator and a
denominator to form a rational
number.

To enable us to implement the concrete level of our data
abstraction, our language provides a compound structure called a
pair
, which can be constructed with the primitive procedure
cons
. This procedure takes two arguments and returns a compound data
object that contains the two arguments as parts. Given a pair, we can
extract the parts using the primitive procedures
car
and
cdr
.
²
Thus, we can use
cons
,
car
, and
cdr
as follows:

(define x (cons 1 2))
(car x)
1
(cdr x)
2

Notice that a pair is a data object that can be given a name and
manipulated, just like a primitive data object. Moreover,
cons
can be used to form pairs whose elements are pairs, and so on:

(define x (cons 1 2))
(define y (cons 3 4))
(define z (cons x y))
(car (car z))
1
(car (cdr z))
3

In section 
2.2
we will see how this ability to
combine pairs means that pairs can be used as general-purpose building
blocks to create all sorts of complex data structures. The single
compound-data primitive
pair
, implemented by the procedures
cons
,
car
, and
cdr
, is the only glue we need. Data
objects constructed from pairs are called
list-structured
data.

Pairs offer a natural way to complete the rational-number system.
Simply represent a rational number as a pair of two integers: a
numerator and a denominator. Then
make-rat
,
numer
, and
denom
are readily implemented as follows:
³

(define (make-rat n d) (cons n d))
(define (numer x) (car x))
(define (denom x) (cdr x))

Also, in order to display the results of our computations,
we can
print rational numbers by printing the numerator, a
slash, and the denominator:
⁴

(define (print-rat x)
  (newline)
  (display (numer x))
  (display "/")
  (display (denom x)))

Now we can try our rational-number procedures:

(define one-half (make-rat 1 2))
(print-rat one-half)
1/2
(define one-third (make-rat 1 3))
(print-rat (add-rat one-half one-third))
5/6
(print-rat (mul-rat one-half one-third))
1/6
(print-rat (add-rat one-third one-third))
6/9

As the final example shows, our rational-number implementation does
not reduce rational numbers to lowest terms. We can remedy this by
changing
make-rat
. If we have a
gcd
procedure like the one
in section 
1.2.5
that produces the greatest common divisor of two
integers, we can use
gcd
to reduce the numerator and the
denominator to lowest terms before constructing the pair:

(define (make-rat n d)
  (let ((g (gcd n d)))
    (cons (/ n g) (/ d g))))

Now we have

(print-rat (add-rat one-third one-third))
2/3

as desired. This modification was accomplished by changing the
constructor
make-rat
without changing any of the procedures
(such as
add-rat
and
mul-rat
)
that implement the actual operations.

Exercise 2.1.
  Define a better version of
make-rat
that
handles both positive and negative arguments.
Make-rat
should
normalize the sign so that if the rational number is positive, both
the numerator and denominator are positive, and if the rational number
is negative, only the numerator is negative.

Before continuing with more examples of compound data and data
abstraction, let us consider some of the issues raised by the
rational-number example. We defined the rational-number operations in
terms of a constructor
make-rat
and selectors
numer
and
denom
. In general, the underlying idea of data abstraction is
to identify for each type of data object a basic set of operations in
terms of which all manipulations of data objects of that type will be
expressed, and then to use only those operations in manipulating the
data.

We can envision the structure of the rational-number system as
shown in figure 
2.1
. The
horizontal lines represent
abstraction barriers
that isolate
different “levels” of the system. At each level, the barrier
separates the programs (above) that use the data abstraction from the
programs (below) that implement the data abstraction. Programs that
use rational numbers manipulate them solely in terms of the procedures
supplied “for public use” by the rational-number package:
add-rat
,
sub-rat
,
mul-rat
,
div-rat
, and
equal-rat?
. These, in turn, are implemented solely in terms of the
constructor and selectors
make-rat
,
numer
, and
denom
, which themselves are implemented in terms of pairs. The
details of how pairs are implemented are irrelevant to the rest of the
rational-number package so long as pairs can be manipulated by the use
of
cons
,
car
, and
cdr
. In effect, procedures at
each level are the interfaces that define the abstraction barriers and
connect the different levels.

Figure 2.1:
  Data-abstraction barriers in the rational-number package.

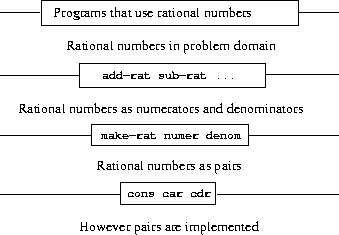This simple idea has many advantages. One advantage is that it makes
programs much easier to maintain and to modify. Any complex data
structure can be represented in a variety of ways with the primitive
data structures provided by a programming language. Of course, the
choice of representation influences the programs that operate on it;
thus, if the representation were to be changed at some later time, all
such programs might have to be modified accordingly. This task could
be time-consuming and expensive in the case of large programs unless
the dependence on the representation were to be confined by design to
a very few program modules.

For example, an alternate way to address the problem of reducing rational
numbers to lowest terms is to perform the reduction whenever we
access the parts of a rational number, rather than when we construct
it. This leads to different constructor and selector procedures:

(define (make-rat n d)
  (cons n d))
(define (numer x)
  (let ((g (gcd (car x) (cdr x))))
    (/ (car x) g)))
(define (denom x)
  (let ((g (gcd (car x) (cdr x))))
    (/ (cdr x) g)))

The difference between this implementation and the previous one lies
in when we compute the
gcd
.
If in our typical use of rational numbers we access the
numerators and denominators of the same rational numbers many
times, it would be preferable
to compute the
gcd
when the rational numbers are constructed.
If not, we may be better off waiting until access
time to compute the
gcd
. In any case, when
we change from one representation to the other, the procedures
add-rat
,
sub-rat
, and so on do not have to be modified at all.

Constraining the dependence on the representation to a few interface
procedures helps us design programs as well as modify them,
because it allows us to maintain the flexibility to consider alternate
implementations. To continue with our simple example, suppose we are
designing a rational-number package and we can't decide initially
whether to perform the
gcd
at construction time or at selection
time. The data-abstraction methodology gives us a way to defer that
decision without losing the ability to make progress on the rest of
the system.

Exercise 2.2.
  Consider the problem of representing
line segments in a plane. Each segment is
represented as a pair of points: a starting point and an ending point.
Define a constructor
make-segment
and selectors
start-segment
and
end-segment
that define the representation of segments in
terms of points. Furthermore, a point
can be represented as a pair
of numbers: the
x
coordinate and the
y
coordinate. Accordingly,
specify a constructor
make-point
and selectors
x-point
and
y-point
that define this representation. Finally, using your
selectors and constructors, define a procedure
midpoint-segment
that takes a line segment as argument and returns its midpoint (the
point whose coordinates are the average of the coordinates of the
endpoints).
To try your procedures, you'll need a way to print points:

(define (print-point p)
  (newline)
  (display "(")
  (display (x-point p))
  (display ",")
  (display (y-point p))
  (display ")"))

Exercise 2.3.
  
Implement a representation for rectangles in a plane.
(Hint: You may want to make use of exercise 
2.2
.)
In terms of
your constructors and selectors, create procedures that compute the
perimeter and the area of a given rectangle. Now implement a
different representation for rectangles. Can you design your system
with suitable abstraction barriers, so that the same perimeter and
area procedures will work using either representation?

We began the rational-number implementation in
section 
2.1.1
by implementing the rational-number
operations
add-rat
,
sub-rat
, and so on in terms of three
unspecified procedures:
make-rat
,
numer
, and
denom
.
At that point, we could think of the operations as being defined in
terms of data objects – numerators, denominators, and rational
numbers – whose behavior was specified by the latter three procedures.