Structure and Interpretation of Computer Programs (14 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

(accumulate combiner null-value term a next b)
Accumulate
takes as arguments the same term and range
specifications as
sum
and
product
, together with a
combiner
procedure (of two arguments) that specifies how the current
term is to be combined with the accumulation of the preceding terms
and a
null-value
that specifies what base value to use
when the terms run out. Write
accumulate
and show how
sum
and
product
can both
be defined as simple calls to
accumulate
.
b. If your
accumulate
procedure generates a recursive process, write one that generates
an iterative process.
If it generates an iterative process, write one that generates
a recursive process.
Exercise 1.33.
You can obtain an even more general version of
accumulate
(exercise
1.32
) by introducing the notion of a
filter
on the terms to be combined. That is, combine only those
terms derived from values in the range that satisfy a specified
condition. The resulting
filtered-accumulate
abstraction takes
the same arguments as accumulate, together with an additional
predicate of one argument that specifies the filter. Write
filtered-accumulate
as a procedure. Show how to express the
following using
filtered-accumulate
:
a. the sum of the squares of the prime numbers in the interval
a
to
b
(assuming that you have a
prime?
predicate already written)
b. the product of all the positive integers less than
n
that are relatively prime to
n
(i.e., all positive integers
i
<
n
such that
G
C
D
(
i
,
n
) = 1).
Lambda
In using
sum
as in section
1.3.1
,
it seems terribly awkward to have to define trivial procedures such as
pi-term
and
pi-next
just so we can use them as arguments to
our higher-order procedure. Rather than define
pi-next
and
pi-term
, it would be more convenient
to have a way to directly specify “the procedure that returns its
input incremented by 4” and “the procedure that returns the
reciprocal of its input times its input plus 2.” We can do this by
introducing the special form
lambda
, which creates procedures.
Using
lambda
we can describe what we want as
(lambda (x) (+ x 4))
and
(lambda (x) (/ 1.0 (* x (+ x 2))))
Then our
pi-sum
procedure can be expressed without defining any
auxiliary procedures as
(define (pi-sum a b)
(sum (lambda (x) (/ 1.0 (* x (+ x 2))))
a
(lambda (x) (+ x 4))
b))
Again using
lambda
, we can write the
integral
procedure
without having to define the auxiliary procedure
add-dx
:
(define (integral f a b dx)
(* (sum f
(+ a (/ dx 2.0))
(lambda (x) (+ x dx))
b)
dx))
In general,
lambda
is used to create procedures in the same way as
define
, except that
no name is specified for the procedure:
(lambda (<
formal-parameters
>) <
body
>)
The resulting procedure is just as much a procedure as one that is
created using
define
. The only difference is that it has not
been associated with any name in the environment. In fact,
(define (plus4 x) (+ x 4))
is equivalent to
(define plus4 (lambda (x) (+ x 4)))
We can read a
lambda
expression as follows:
(lambda (x) (+ x 4))
↑ ↑ ↑ ↑ ↑
the procedure of an argument
x
that adds
x
and 4
Like any expression that has a procedure as its value, a
lambda
expression can be used as the operator in a combination such as
((lambda (x y z) (+ x y (square z))) 1 2 3)
12
or, more generally, in any context where we would normally use a
procedure name.
53
let
to create local variables
Another use of
lambda
is in creating local variables.
We often need local variables in our procedures other than those that have
been bound as formal parameters. For example, suppose we wish to
compute the function
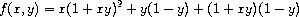
which we could also express as
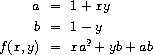
In writing a procedure to compute
f
, we would like to include as
local variables not only
x
and
y
but also the names of
intermediate quantities like
a
and
b
. One way to
accomplish this is to
use an auxiliary procedure to bind the local variables:
(define (f x y)
(define (f-helper a b)
(+ (* x (square a))
(* y b)
(* a b)))
(f-helper (+ 1 (* x y))
(- 1 y)))
Of course, we could use a
lambda
expression to specify an
anonymous procedure for binding our local variables. The body of
f
then becomes a single call to that procedure:
(define (f x y)
((lambda (a b)
(+ (* x (square a))
(* y b)
(* a b)))
(+ 1 (* x y))
(- 1 y)))
This construct is so useful that there is a special form called
let
to make its use more convenient. Using
let
, the
f
procedure could be written as
(define (f x y)
(let ((a (+ 1 (* x y)))
(b (- 1 y)))
(+ (* x (square a))
(* y b)
(* a b))))
The general form of a
let
expression is
(let ((<
var
1
> <
exp
1
>)
(<
var
2
> <
exp
2
>)
⋮
(<
var
n
> <
exp
n
>))
<
body
>)
which can be thought of as saying
| let | < var 1 > have the value < exp 1 > and |
| < var 2 > have the value < exp 2 > and | |
| ⋮ | |
| < var n > have the value < exp n > | |
| in | < body > |
The first part of the
let
expression is a list of
name-expression pairs. When the
let
is evaluated, each name is
associated with the value of the corresponding expression. The body
of the
let
is evaluated with
these names bound as local variables. The way this happens is that the
let
expression is interpreted as an alternate syntax for
((lambda (<
var
1
>
...
<
var
n
>)
<
body
>)
<
exp
1
>
⋮
<
exp
n
>)
No new mechanism is required in the interpreter in order to
provide local variables. A
let
expression is simply syntactic sugar for
the underlying
lambda
application.
We can see from this equivalence that
the scope of a variable specified by a
let
expression is the body of
the
let
.
This implies that:
- Let
allows one to
bind variables as locally as possible to where they
are to be used. For example, if the value of
x
is 5,
the value of the expression(+ (let ((x 3))
(+ x (* x 10)))
x)is 38. Here, the
x
in the body of the
let
is 3,
so the value of the
let
expression is 33. On the other hand, the
x
that is the second argument to the outermost
+
is still 5. - The variables' values are computed outside the
let
.
This matters when the expressions that
provide the values for the local variables depend upon
variables having the same names as the local variables themselves.
For example, if the value of
x
is 2, the expression(let ((x 3)
(y (+ x 2)))
(* x y))will have the value 12 because, inside the body of the
let
,
x
will be 3 and
y
will be 4 (which is the
outer
x
plus 2).
Sometimes we can use internal definitions to get the same effect as
with
let
. For example, we could have defined the procedure
f
above as
(define (f x y)
(define a (+ 1 (* x y)))
(define b (- 1 y))
(+ (* x (square a))
(* y b)
(* a b)))
We prefer, however, to use
let
in situations like this
and to use internal
define
only for internal procedures.
54
Exercise 1.34.
Suppose we define the procedure
(define (f g)
(g 2))
Then we have
(f square)
4
(f (lambda (z) (* z (+ z 1))))
6
What happens if we (perversely) ask the interpreter to evaluate the
combination
(f f)
? Explain.
We introduced compound procedures in
section
1.1.4
as a mechanism for abstracting
patterns of numerical operations so as to make them independent of the
particular numbers involved. With higher-order procedures, such as
the
integral
procedure of
section
1.3.1
, we began to see a more
powerful kind of abstraction: procedures used to express general
methods of computation, independent of the particular functions
involved. In this section we discuss two more elaborate
examples – general methods for finding zeros and fixed points of
functions – and show how these methods can be expressed directly as
procedures.
The
half-interval method
is a simple but powerful technique for
finding roots of an equation
f
(
x
) = 0, where
f
is a continuous
function. The idea is that, if we are given points
a
and
b
such
that
f
(
a
) < 0 <
f
(
b
), then
f
must have at least one zero between
a
and
b
. To locate a zero, let
x
be the average of
a
and
b
and compute
f
(
x
). If
f
(
x
) > 0, then
f
must have a zero between
a
and
x
. If
f
(
x
) < 0, then
f
must have a zero between
x
and
b
. Continuing in this way, we can identify smaller and smaller
intervals on which
f
must have a zero. When we reach a point where
the interval is small enough, the process stops. Since the interval
of uncertainty is reduced by half at each step of the process, the
number of steps required grows as θ(
log
(
L
/
T
)), where
L
is the
length of the original interval and
T
is the error tolerance
(that is, the size of the interval we will consider “small enough”).
Here is a procedure that implements this strategy: