Structure and Interpretation of Computer Programs (9 page)

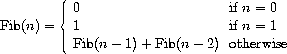
We can immediately translate this definition into a recursive
procedure for computing Fibonacci numbers:

(define (fib n)
  (cond ((= n 0) 0)
        ((= n 1) 1)
        (else (+ (fib (- n 1))
                 (fib (- n 2))))))

Figure 1.5:
  The tree-recursive process generated in computing
(fib 5)
.

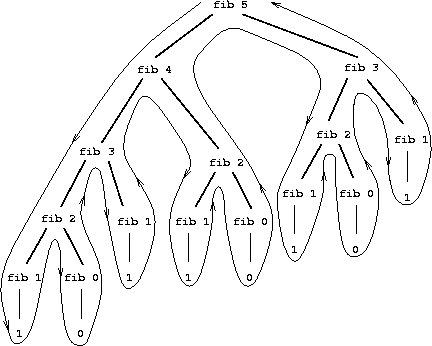Consider the pattern of this computation. To compute
(fib 5)
,
we compute
(fib 4)
and
(fib 3)
. To compute
(fib 4)
,
we compute
(fib 3)
and
(fib 2)
. In general, the evolved
process looks like a tree, as shown in figure 
1.5
.
Notice that the branches split into two at each level (except at the
bottom); this reflects the fact that the
fib
procedure calls
itself twice each time it is invoked.

This procedure is instructive as a prototypical tree recursion, but it
is a terrible way to compute Fibonacci numbers because it does so much
redundant computation. Notice in figure 
1.5
that
the entire computation of
(fib 3)
– almost half the work – is
duplicated. In fact, it is not hard to show that the number of times
the procedure will compute
(fib 1)
or
(fib 0)
(the number
of leaves in the above tree, in general) is precisely
F
i
b
(
n
+ 1). To get an idea of how bad this is, one can show that the
value of
F
i
b
(
n
)
grows exponentially with
n
. More precisely
(see exercise 
1.13
),
F
i
b
(
n
) is the closest
integer to
φ
ⁿ
/√5, where

φ
= (1 + √5)/2 ≈ 1.6180

is the
golden ratio
, which satisfies the equation

φ
²
=
φ
+ 1

Thus, the process uses a number of steps that grows exponentially
with the input. On the other hand, the space required grows only
linearly with the input, because we need keep track only of which
nodes are above us in the tree at any point in the computation. In
general, the number of steps required by a tree-recursive process will be
proportional to the number of nodes in the tree, while the space
required will be proportional to the maximum depth of the tree.

We can also formulate an iterative process for computing the
Fibonacci numbers. The idea is to use a pair of integers
a
and
b
, initialized to
F
i
b
(1) = 1 and
F
i
b
(0) = 0,
and to repeatedly apply the simultaneous
transformations

a
⟵
a
+
b
b
⟵
a

(define (fib n)
  (fib-iter 1 0 n))
(define (fib-iter a b count)
  (if (= count 0)
      b
      (fib-iter (+ a b) a (- count 1))))

This second method for computing
F
i
b
(
n
) is a linear iteration. The
difference in number of steps required by the two methods – one linear in
n
,
one growing as fast as
F
i
b
(
n
) itself – is enormous, even for
small inputs.

One should not conclude from this that tree-recursive processes are
useless. When we consider processes that operate on hierarchically
structured data rather than numbers, we will find that tree recursion
is a natural and powerful tool.
³²
But even in numerical operations,
tree-recursive processes can be useful in helping us to understand and
design programs. For instance, although the first
fib
procedure
is much less efficient than the second one, it is more
straightforward, being little more than a translation into Lisp of the
definition of the Fibonacci sequence. To formulate the iterative
algorithm required noticing that the computation could be recast as an
iteration with three state variables.

It takes only a bit of cleverness to come up with the iterative
Fibonacci algorithm. In contrast, consider the
following problem: How many different ways can we make change of $ 1.00,
given half-dollars, quarters, dimes, nickels, and pennies? More
generally, can we write a procedure to compute the number of ways to
change any given amount of money?

This problem has a simple solution as a recursive procedure. Suppose
we think of the types of coins available as arranged in some order.
Then the following relation holds:

The number of ways to change amount
a
using
n
kinds of coins equals

• the number of ways to change amount
  a
  using all but the first
  kind of coin, plus
  
• the number of ways to change amount
  a
  -
  d
  using all
  n
  kinds of
  coins, where
  d
  is the denomination of the first kind of coin.
  

To see why this is true, observe that the ways to make change can be
divided into two groups: those that do not use any of the first kind
of coin, and those that do. Therefore, the total number of ways to
make change for some amount is equal to the number of ways to make
change for the amount without using any of the first kind of coin,
plus the number of ways to make change assuming that we do use the
first kind of coin. But the latter number is equal to the number of
ways to make change for the amount that remains after using a coin of
the first kind.

Thus, we can recursively reduce the problem of changing a given amount
to the problem of changing smaller amounts using fewer kinds of coins.
Consider this reduction rule carefully, and convince yourself that we
can use it to describe an algorithm if we specify the following
degenerate cases:
³³

• If
  a
  is exactly 0, we should count that as 1 way to make change.
  
• If
  a
  is less than 0, we should count that as 0 ways to make change.
  
• If
  n
  is 0, we should count that as 0 ways to make change.
  

We can easily translate this description into a recursive
procedure:

(define (count-change amount)
  (cc amount 5))
(define (cc amount kinds-of-coins)
  (cond ((= amount 0) 1)
        ((or (< amount 0) (= kinds-of-coins 0)) 0)
        (else (+ (cc amount
                     (- kinds-of-coins 1))
                 (cc (- amount
                        (first-denomination kinds-of-coins))
                     kinds-of-coins)))))
(define (first-denomination kinds-of-coins)
  (cond ((= kinds-of-coins 1) 1)
        ((= kinds-of-coins 2) 5)
        ((= kinds-of-coins 3) 10)
        ((= kinds-of-coins 4) 25)
        ((= kinds-of-coins 5) 50)))

(The
first-denomination
procedure takes as input the number of
kinds of coins available and returns the denomination of the first
kind. Here we are thinking of the coins as arranged in order from
largest to smallest, but any order would do as well.) We can now
answer our original question about changing a dollar:

(count-change 100)
292

Count-change
generates a tree-recursive process with
redundancies similar to those in our first implementation of
fib
. (It will take quite a while for that 292 to be computed.) On
the other hand, it is not obvious how to design a better algorithm
for computing the result, and we leave this problem as a challenge.
The observation that a
tree-recursive process may be highly
inefficient but often easy to specify and understand has led people to
propose that one could get the best of both worlds by designing a
“smart compiler” that could transform tree-recursive procedures into
more efficient procedures that compute the same result.
³⁴

Exercise 1.11.
  A function
f
is defined by the rule that
f
(
n
) =
n
if
n
<3 and
f
(
n
) =
f
(
n
- 1) + 2
f
(
n
- 2) + 3
f
(
n
- 3) if
n
>
3. Write a procedure that
computes
f
by means of a recursive process. Write a procedure that
computes
f
by means of an iterative process.

Exercise 1.12.
  
The following pattern of numbers is called
Pascal's triangle
.

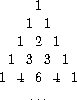
The numbers at the edge of the triangle are all 1, and
each number inside the triangle is the sum of the two numbers above it.
³⁵
Write a procedure that computes elements of Pascal's triangle by means
of a recursive process.

Exercise 1.13.
  Prove that
F
i
b
(
n
) is the closest integer to
φ
ⁿ
/√5,
where
φ
= (1 + √5)/2. Hint: Let
ψ
= (1 - √5)/2. Use
induction and the definition of the Fibonacci numbers (see
section 
1.2.2
) to prove that
F
i
b
(
n
) = (
φ
ⁿ
-
ψ
ⁿ
)/√5.

The previous examples illustrate that processes can differ
considerably in the rates at which they consume computational
resources. One convenient way to describe this difference is to use
the notion of
order of growth
to obtain a gross measure of the
resources required by a process as the inputs become larger.

Let
n
be a parameter that measures the size of the problem, and let
R
(
n
) be the amount of resources the process requires for a problem
of size
n
. In our previous examples we took
n
to be the number
for which a given function is to be computed, but there are other
possibilities. For instance, if our goal is to compute an
approximation to the square root of a number, we might take
n
to be
the number of digits accuracy required. For matrix multiplication we
might take
n
to be the number of rows in the matrices. In general
there are a number of properties of the problem with respect to which
it will be desirable to analyze a given process. Similarly,
R
(
n
)
might measure the number of internal storage registers used, the
number of elementary machine operations performed, and so on. In
computers that do only a fixed number of operations at a time, the
time required will be proportional to the number of elementary machine
operations performed.