Structure and Interpretation of Computer Programs (4 page)

In this chapter we will deal only with simple
numerical data so that
we can focus on the rules for building procedures.
⁴
In later chapters we will see that
these same rules allow us to build procedures to manipulate compound
data as well.

One easy way to get started at programming is to examine some typical
interactions with an interpreter for the Scheme dialect of Lisp.
Imagine that you are sitting at a computer terminal. You type an
expression
, and the interpreter responds by displaying the result of
its
evaluating
that expression.

One kind of primitive expression you might type is a number. (More
precisely, the expression that you type consists of the numerals that
represent the number in base 10.) If you present Lisp with
a number

486

the interpreter will respond by printing
⁵

486

Expressions representing numbers may be combined with an
expression
representing a
primitive procedure (such as
+
or
*
) to form a
compound expression that represents the
application of the procedure to those numbers. For example:

(+ 137 349)
486
(- 1000 334)
666
(* 5 99)
495
(/ 10 5)
2
(+ 2.7 10)
12.7

Expressions such as these, formed by
delimiting a list of expressions
within parentheses in order to denote
procedure application,
are called
combinations
. The leftmost
element in the list is called the
operator
, and the other
elements are called
operands
. The
value of a combination is
obtained by applying the procedure specified by the operator to the
arguments
that are the values of the operands.

The convention of placing the operator to the left of the operands is
known as
prefix notation
, and it may be somewhat confusing at
first because it departs significantly from the customary mathematical
convention. Prefix notation has several advantages, however. One of
them is that it can accommodate
procedures that may take an arbitrary
number of arguments, as in the following examples:

(+ 21 35 12 7)
75
(* 25 4 12)
1200

No ambiguity can arise, because the operator is always the leftmost
element and the entire combination is delimited by the
parentheses.

A second advantage of prefix notation is that it extends in a
straightforward way to allow combinations to be
nested
, that is,
to have combinations whose elements are themselves
combinations:

(+ (* 3 5) (- 10 6))
19

There is no limit (in principle) to the depth of such nesting and to
the overall complexity of the expressions that the Lisp interpreter
can evaluate.
It is we humans who get confused by still relatively
simple expressions such as

(+ (* 3 (+ (* 2 4) (+ 3 5))) (+ (- 10 7) 6))

which the interpreter would readily evaluate to be 57. We can help
ourselves by writing such an expression in the form

(+ (* 3
      (+ (* 2 4)
         (+ 3 5)))
   (+ (- 10 7)
      6))

following a formatting convention known as
pretty-printing
, in
which each long combination is written so that the operands are
aligned vertically. The resulting indentations display clearly the
structure of the expression.
⁶

Even with complex expressions, the interpreter always operates in the
same basic cycle: It reads an expression from the terminal,
evaluates the expression, and prints the result.
This mode of operation is often expressed by saying that the
interpreter runs in a
read-eval-print loop
.
Observe in particular that it is not necessary to explicitly
instruct the interpreter to print the value of the expression.
⁷

A critical aspect of a programming language is the means it provides
for using
names to refer to computational objects. We say that the
name identifies a
variable
whose
value
is the object.

In the Scheme dialect of Lisp, we
name things with
define
. Typing

(define size 2)

causes the interpreter to associate the value 2 with the
name
size
.
⁸
Once the name
size
has been associated with the number 2, we can
refer to the value 2 by name:

size
2
(* 5 size)
10

Here are further examples of the use of
define
:

(define pi 3.14159)
(define radius 10)
(* pi (* radius radius))
314.159
(define circumference (* 2 pi radius))
circumference
62.8318

Define
is our language's
simplest means of abstraction, for it allows us to use simple names to
refer to the results of compound operations, such as the
circumference
computed above.
In general, computational objects may have very complex
structures, and it would be extremely inconvenient to have to remember
and repeat their details each time we want to use them. Indeed,
complex programs are constructed by building, step by step,
computational objects of increasing complexity. The
interpreter makes this step-by-step program construction particularly
convenient because name-object associations can be created
incrementally in successive interactions. This feature encourages the
incremental development and testing of programs and is largely
responsible for the fact that
a Lisp program usually consists of a large
number of relatively simple procedures.

It should be clear that the possibility of associating values with
symbols and later retrieving them means that the interpreter must
maintain some sort of memory that keeps track of the name-object
pairs. This memory is called the
environment
(more precisely
the
global environment
, since we will see later that a
computation may involve a number of different
environments).
⁹

One of our goals in this chapter is to isolate issues about thinking
procedurally. As a case in point, let us consider that, in evaluating
combinations, the interpreter is itself following a procedure.

• To evaluate a combination, do the following:
  

1.  Evaluate the subexpressions of the combination.

2.  Apply the procedure that is the value of the leftmost
subexpression (the operator) to the arguments that are the values of
the other subexpressions (the operands).

Even this simple rule illustrates some important points about
processes in general. First, observe that the first step dictates
that in order to accomplish the evaluation process for a combination
we must first perform the evaluation process on each element of the
combination. Thus, the evaluation rule is
recursive
in nature;
that is, it includes, as one of its steps, the need to invoke the rule
itself.
¹⁰

Notice how succinctly the idea of recursion can be used to express
what, in the case of a deeply nested combination, would otherwise be
viewed as a rather complicated process. For example, evaluating

(* (+ 2 (* 4 6))
   (+ 3 5 7))

requires that the evaluation rule be applied to four different
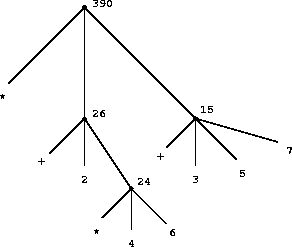
combinations. We can obtain a picture of this process by
representing
the combination in the form of a
tree, as shown in
figure 
1.1
. Each combination is represented by a
node with
branches corresponding to the operator and the
operands of the combination stemming from it.
The
terminal nodes (that is, nodes with
no branches stemming from them) represent either operators or numbers.
Viewing evaluation in terms of the tree, we can imagine that the
values of the operands percolate upward, starting from the terminal
nodes and then combining at higher and higher levels. In general, we
shall see that recursion is a very powerful technique for dealing with
hierarchical, treelike objects. In fact, the “percolate values
upward” form of the evaluation rule is an example of a general kind
of process known as
tree accumulation
.

Figure 1.1:
  Tree representation, showing the value of each subcombination.

Next, observe that the repeated application of the first step brings
us to the point where we need to evaluate, not combinations, but
primitive expressions such as numerals, built-in operators, or other
names. We take care of the primitive cases by stipulating that

• the values of numerals are the numbers that they name,
  
• the values of built-in operators are the machine
  instruction sequences that carry out the corresponding operations, and
  
• the values of other names are the objects associated
  with those names in the environment.
  

We may regard the second rule as a special case of the third one by
stipulating that symbols such as
+
and
*
are also included
in the global environment, and are associated with the sequences of
machine instructions that are their “values.” The key point to
notice is the role of the
environment in determining the meaning of
the symbols in expressions. In an interactive language such as
Lisp, it is meaningless to speak of the value of an expression such as
(+ x 1)
without specifying any information about the environment
that would provide a meaning for the symbol 
x
(or even for the
symbol
+
). As we shall see in chapter 3, the general notion of
the environment as providing a context in which evaluation takes place
will play an important role in our understanding of program execution.

Notice that the
evaluation rule given above does not handle definitions.
For instance, evaluating
(define x 3)
does not apply
define
to two arguments, one
of which is the value of the symbol
x
and the other of which is
3, since the purpose of the
define
is precisely to associate
x
with a value.
(That is,
(define x 3)
is not a combination.)

Such exceptions to the general evaluation rule are called
special
forms
.
Define
is the only example of a special form that we
have seen so far, but we will meet others shortly.
Each special form
has its own evaluation rule. The various kinds of expressions (each
with its associated evaluation rule) constitute the
syntax of the
programming language. In comparison with most other programming
languages, Lisp has a very simple syntax; that is, the evaluation rule
for expressions can be described by a simple general rule together
with specialized rules for a small number of special
forms.
¹¹

We have identified in Lisp some of the elements that must appear in
any powerful programming language:

• Numbers and arithmetic operations are
  primitive data and procedures.
  
• Nesting of combinations provides a means of
  combining operations.
  
• Definitions that associate names with values provide a
  limited means of abstraction.
  

Now we will learn about
procedure definitions
, a much more powerful abstraction
technique by which a compound operation can be given a name and then
referred to as a unit.

We begin by examining how to express the idea of “squaring.” We
might say, “To square something, multiply it by itself.” This is
expressed in our language as

(define (square x) (* x x))

We can understand this in the following way:

(define (square  x)        (*         x     x))
   ↑        ↑     ↑          ↑         ↑    ↑
 To      square something, multiply   it by itself.

We have here a
compound procedure
, which has been given the name
square
. The procedure represents the operation of multiplying
something by itself. The thing to be multiplied is given a local
name,
x
, which plays the same role that a pronoun plays in
natural language.
Evaluating the definition creates this
compound procedure and associates it with the name
square
.
¹²

The general form of a procedure definition is

(define (<
name
> <
formal parameters
>) <
body
>)