Structure and Interpretation of Computer Programs (5 page)

The <
name
> is a symbol to be associated with the procedure
definition in the environment.
¹³
The
<
formal parameters
> are
the names used within the body of the procedure to refer to the
corresponding arguments of the procedure. The
<
body
> is an expression that will yield the value of
the procedure application when the formal parameters are replaced by
the actual arguments to which the procedure is applied.
¹⁴
The <
name
>
and the <
formal parameters
>
are grouped within
parentheses, just as they
would be in an actual call to the procedure being defined.

Having defined
square
, we can now use it:

(square 21)
441
(square (+ 2 5))
49
(square (square 3))
81

We can also use
square
as a building block in defining other
procedures. For example,
x
²
+
y
²
can be expressed as

(+ (square x) (square y))

We can easily define a procedure
sum-of-squares
that, given any two numbers as arguments, produces the
sum of their squares:

(define (sum-of-squares x y)
  (+ (square x) (square y)))
(sum-of-squares 3 4)
25

Now we can use
sum-of-squares
as a building block in constructing
further procedures:

(define (f a)
  (sum-of-squares (+ a 1) (* a 2)))
(f 5)
136

Compound procedures are used in exactly the same way as primitive
procedures. Indeed, one could not tell by looking at the definition
of
sum-of-squares
given above whether
square
was built into
the interpreter, like
+
and
*
, or defined as a compound procedure.

To evaluate a combination whose operator names a compound procedure, the
interpreter follows much the same process as for combinations whose
operators name primitive procedures, which we described in
section 
1.1.3
. That is, the interpreter
evaluates the elements of the combination and applies the procedure
(which is the value of the operator of the combination) to the
arguments (which are the values of the operands of the combination).

We can assume that the mechanism for applying primitive procedures to
arguments is built into the interpreter. For compound procedures, the
application process is as follows:

• To apply a compound procedure to arguments, evaluate the body of the
  procedure with each formal parameter replaced by the corresponding
  argument.
  

To illustrate this process, let's evaluate the combination

(f 5)

where
f
is the procedure defined in
section 
1.1.4
. We begin by retrieving the
body of
f
:

(sum-of-squares (+ a 1) (* a 2))

Then we replace the formal parameter
a
by the argument 5:

(sum-of-squares (+ 5 1) (* 5 2))

Thus the problem reduces to the evaluation of a combination with two
operands and an operator
sum-of-squares
. Evaluating this
combination involves three subproblems. We must evaluate the
operator to get the procedure to be applied, and we must evaluate the
operands to get the arguments. Now
(+ 5 1)
produces 6 and
(* 5 2)
produces 10, so we must apply the
sum-of-squares
procedure to 6 and 10. These values are substituted
for the formal parameters
x
and
y
in the body of
sum-of-squares
,
reducing the expression to

(+ (square 6) (square 10))

If we use the definition of
square
, this reduces to

(+ (* 6 6) (* 10 10))

which reduces by multiplication to

(+ 36 100)

and finally to

136

The process we have just described is called the
substitution
model
for procedure application. It can be taken as a model that
determines the “meaning” of procedure application, insofar as the
procedures in this chapter are concerned. However, there are two
points that should be stressed:

• The purpose of the substitution is to help us think about
  procedure application, not to provide a description of how
  the interpreter really works. Typical interpreters do not evaluate
  procedure applications by manipulating the text of a procedure to
  substitute values for the formal parameters. In practice, the
  “substitution” is accomplished by using a local environment for the
  formal parameters. We will discuss this more fully in chapters 3 and
  4 when we examine the implementation of an interpreter in detail.
  
• Over the course of this book, we will present a sequence of
  increasingly elaborate models of how interpreters work, culminating
  with a complete implementation of an interpreter and compiler in
  chapter 5. The substitution model is only the first of these
  models – a way to get started thinking formally about the evaluation
  process. In general, when
  modeling phenomena in science and
  engineering, we begin with simplified, incomplete models. As we
  examine things in greater detail, these simple models become
  inadequate and must be replaced by more refined models. The
  substitution model is no exception. In particular, when we address in
  chapter 3 the use of procedures with “mutable data,” we will see that
  the substitution model breaks down and must be replaced by a more
  complicated model of procedure application.
  ¹⁵
  

According to the description of evaluation given in
section 
1.1.3
, the interpreter first
evaluates the operator and operands and then applies the resulting procedure
to the resulting arguments. This is not the only way to perform
evaluation. An alternative evaluation model would not evaluate the
operands until their values were needed. Instead it would first substitute
operand expressions for parameters until
it obtained an expression involving only primitive operators, and
would then perform the evaluation. If we used this method, the
evaluation of

(f 5)

would proceed according to the sequence of expansions

(sum-of-squares (+ 5 1) (* 5 2))
(+    (square (+ 5 1))      (square (* 5 2))  )
(+    (* (+ 5 1) (+ 5 1))   (* (* 5 2) (* 5 2)))

followed by the reductions

(+         (* 6 6)             (* 10 10))
(+           36                   100)
                    136

This gives the same answer as our previous evaluation model, but the
process is different. In particular, the evaluations
of
(+ 5 1)
and
(* 5 2)
are each performed twice here,
corresponding to the reduction of the expression

(* x x)

with
x
replaced respectively by
(+ 5 1)
and
(* 5 2)
.

This alternative “fully expand and then reduce” evaluation method is
known as
normal-order evaluation
, in contrast to the “evaluate
the arguments and then apply” method that the interpreter actually
uses, which is called
applicative-order evaluation
. It can be
shown that, for procedure applications that can be modeled using
substitution (including all the procedures in the first two chapters
of this book) and that yield legitimate values, normal-order and
applicative-order evaluation produce the same value. (See
exercise 
1.5
for an instance of
an “illegitimate” value where normal-order and applicative-order
evaluation do not give the same result.)

Lisp uses applicative-order evaluation, partly because of the
additional efficiency obtained from avoiding multiple evaluations of
expressions such as those illustrated with
(+ 5 1)
and
(* 5
2)
above and, more significantly, because normal-order evaluation
becomes much more complicated to deal with when we leave the realm of
procedures that can be modeled by substitution. On the other hand,
normal-order evaluation can be an extremely valuable tool, and we will
investigate some of its implications in chapters 3 and 4.
¹⁶

The expressive power of the class of procedures that we can define at
this point is very limited, because we have no way to make tests and
to perform different operations depending on the result of a test.
For instance, we cannot define a procedure that computes the
absolute
value of a number by testing whether the number is positive, negative,
or zero and taking different actions in the different cases according
to the rule

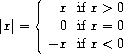
This construct is called a
case analysis
, and
there is a special form in Lisp for notating such a case
analysis. It is called
cond
(which stands for
“conditional”), and it is used as follows:

(define (abs x)
  (cond ((> x 0) x)
        ((= x 0) 0)
        ((< x 0) (- x))))

The general form of a conditional expression is

(cond (<
p
₁
> <
e
₁
>)
      (<
p
₂
> <
e
₂
>)
      ⋮
      (<
p
_n
> <
e
_n
>))

consisting of the symbol
cond
followed by
parenthesized pairs of expressions
(<
p
> <
e
>)
called
clauses
. The first expression in each pair is a
predicate
– that is, an expression whose value is interpreted as
either true or false.
¹⁷

Conditional expressions are evaluated as follows. The predicate
<
p
₁
> is evaluated first. If its value is false, then
<
p
₂
> is evaluated. If <
p
₂
>'s value is also false, then
<
p
₃
> is evaluated. This process continues until a predicate is
found whose value is true, in which case the interpreter returns the
value of the corresponding
consequent expression
<
e
> of the
clause as the value of the conditional expression. If none of the
<
p
>'s is found to be true, the value of the
cond
is
undefined.

The word
predicate
is used for procedures that return true
or false, as well as for expressions that evaluate to true or false.
The absolute-value procedure
abs
makes use of the
primitive
predicates
>
,
<
, and
=
.
¹⁸
These take two
numbers as arguments and test whether the first number is,
respectively, greater than, less than, or equal to the second number,
returning true or false accordingly.

Another way to write the absolute-value procedure is

(define (abs x)
  (cond ((< x 0) (- x))
        (else x)))

which could be expressed in English as “If
x
is less than zero
return -
x
; otherwise return
x
.”
Else
is a special symbol
that can be used in place of the <
p
> in the final clause of a
cond
. This causes the
cond
to return as its value the value of
the corresponding <
e
> whenever all previous clauses have been
bypassed. In fact, any expression that always evaluates to a true
value could be used as the <
p
> here.

Here is yet another way to write the absolute-value procedure:

(define (abs x)
  (if (< x 0)
      (- x)
      x))

This uses the special form
if
, a restricted type of conditional
that can be used when there are precisely
two cases in the case
analysis. The general form of an
if
expression is

(if <
predicate
> <
consequent
> <
alternative
>)

To evaluate an
if
expression, the interpreter starts by evaluating
the
<
predicate
> part of the expression. If the <
predicate
>
evaluates to a true value, the interpreter then evaluates
the
<
consequent
> and returns its value. Otherwise it evaluates
the
<
alternative
> and returns its value.
¹⁹

In addition to primitive
predicates such as
<
,
=
, and
>
, there are logical
composition operations, which enable us to construct compound
predicates. The three most frequently used are these: