Structure and Interpretation of Computer Programs (7 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

Sqrt
is our first example of a process defined by a set of
mutually defined procedures. Notice that the definition of
sqrt-iter
is
recursive
; that is, the procedure is defined in
terms of itself. The idea of being able to define a procedure in
terms of itself may be disturbing; it may seem unclear how such a
“circular” definition could make sense at all, much less specify a
well-defined process to be carried out by a computer. This will be
addressed more carefully in
section
1.2
. But first let's consider
some other important points illustrated by the
sqrt
example.
Observe that the problem of computing square roots breaks up naturally
into a number of subproblems: how to tell whether a guess is good
enough, how to improve a guess, and so on. Each of these tasks is
accomplished by a separate procedure. The entire
sqrt
program
can be viewed as a cluster of procedures (shown in
figure
1.2
) that mirrors the decomposition of
the problem into subproblems.
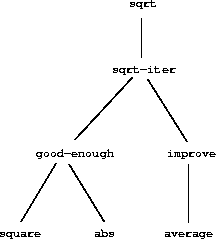 |
The importance of this decomposition strategy is not simply that one
is dividing the program into parts. After all, we could take any
large program and divide it into parts – the first ten lines, the next
ten lines, the next ten lines, and so on. Rather, it is crucial that
each procedure accomplishes an identifiable task that can be used as a
module in defining other procedures.
For example, when we define the
good-enough?
procedure in terms of
square
, we are able to
regard the
square
procedure as a
“black box.” We are not at
that moment concerned with
how
the procedure computes its
result, only with the fact that it computes the square. The details
of how the square is computed can be suppressed, to be considered at a
later time. Indeed, as far as the
good-enough?
procedure is
concerned,
square
is not quite a procedure but rather an
abstraction of a procedure, a so-called
procedural abstraction
.
At this level of abstraction, any procedure that computes the square
is equally good.
Thus, considering only the values they return, the following two procedures for
squaring a number should be indistinguishable. Each takes a numerical
argument and produces the square of that number as the
value.
25
(define (square x) (* x x))
(define (square x)
(exp (double (log x))))
(define (double x) (+ x x))
So a procedure definition should be able to suppress detail. The
users of the procedure may not have written the procedure themselves,
but may have obtained it from another programmer as a black box. A
user should not need to know how the procedure is implemented in order
to use it.
One detail of a procedure's implementation that should not matter to
the user of the procedure is the implementer's choice of names for the
procedure's formal parameters. Thus, the following procedures should
not be distinguishable:
(define (square x) (* x x))
(define (square y) (* y y))
This principle – that the meaning of a procedure should be independent
of the parameter names used by its author – seems on the surface to be
self-evident, but its consequences are profound. The simplest
consequence is that the parameter names of a procedure must be local
to the body of the procedure. For example, we used
square
in
the definition of
good-enough?
in our square-root procedure:
(define (good-enough? guess x)
(< (abs (- (square guess) x)) 0.001))
The intention of the author of
good-enough?
is to determine if
the square of the first argument is within a given tolerance of the
second argument. We see that the author of
good-enough?
used
the name
guess
to refer to the first argument and
x
to
refer to the second argument. The argument of
square
is
guess
. If the author of
square
used
x
(as above)
to refer to that argument, we see that the
x
in
good-enough?
must be a different
x
than the one in
square
. Running the procedure
square
must not affect the value
of
x
that is used by
good-enough?
, because that value of
x
may be needed by
good-enough?
after
square
is done
computing.
If the parameters were not local to the bodies of their respective
procedures, then the parameter
x
in
square
could be
confused with the parameter
x
in
good-enough?
, and the
behavior of
good-enough?
would depend upon which version of
square
we used. Thus,
square
would not be the black box
we desired.
A formal parameter of a procedure has a very special role in the
procedure definition, in that it doesn't matter what name the formal
parameter has. Such a name is called a
bound variable
, and we
say that the procedure definition
binds
its formal parameters.
The meaning of a procedure definition is unchanged if a bound variable
is consistently renamed throughout the definition.
26
If a variable is not bound, we say that it is
free
. The
set of expressions for which a binding defines a name is called the
scope
of that name.
In a procedure definition, the bound variables
declared as the
formal parameters of the procedure have the body of
the procedure as their scope.
In the definition of
good-enough?
above,
guess
and
x
are
bound variables but
<
,
-
,
abs
, and
square
are free.
The meaning of
good-enough?
should be independent of the names we
choose for
guess
and
x
so long as they are distinct and
different from
<
,
-
,
abs
, and
square
. (If we renamed
guess
to
abs
we would have introduced a bug by
capturing
the variable
abs
. It would have changed from free to bound.) The
meaning of
good-enough?
is not independent of the names of its
free variables, however. It surely depends upon the fact (external to
this definition) that the symbol
abs
names a procedure for
computing the absolute value of a number.
Good-enough?
will
compute a different function if we substitute
cos
for
abs
in
its definition.
We have one kind of name isolation available to us so far: The formal
parameters of a procedure are local to the body of the procedure. The
square-root program illustrates another way in which we would like to
control the use of names.
The existing program consists of
separate procedures:
(define (sqrt x)
(sqrt-iter 1.0 x))
(define (sqrt-iter guess x)
(if (good-enough? guess x)
guess
(sqrt-iter (improve guess x) x)))
(define (good-enough? guess x)
(< (abs (- (square guess) x)) 0.001))
(define (improve guess x)
(average guess (/ x guess)))
The problem with this program is that the only procedure that is
important to users of
sqrt
is
sqrt
. The other
procedures (
sqrt-iter
,
good-enough?
, and
improve
)
only clutter up their minds. They may not define any other procedure
called
good-enough?
as part of another program to work together
with the square-root program, because
sqrt
needs it. The
problem is especially severe in the construction of large systems by
many separate programmers. For example, in the construction of a
large library of numerical procedures, many numerical functions are
computed as successive approximations and thus might have procedures
named
good-enough?
and
improve
as auxiliary procedures.
We would like to localize the subprocedures, hiding them inside
sqrt
so that
sqrt
could coexist with other successive
approximations, each having its own private
good-enough?
procedure. To make this possible, we allow a
procedure to have
internal definitions that are local to that procedure. For example,
in the square-root problem we can write
(define (sqrt x)
(define (good-enough? guess x)
(< (abs (- (square guess) x)) 0.001))
(define (improve guess x)
(average guess (/ x guess)))
(define (sqrt-iter guess x)
(if (good-enough? guess x)
guess
(sqrt-iter (improve guess x) x)))
(sqrt-iter 1.0 x))
Such nesting of definitions, called
block structure
,
is basically the right solution to the simplest
name-packaging problem. But there is a better idea lurking here. In
addition to internalizing the definitions of the auxiliary procedures,
we can simplify them. Since
x
is bound in the definition of
sqrt
, the procedures
good-enough?
,
improve
, and
sqrt-iter
, which are defined internally to
sqrt
, are in the
scope of
x
. Thus, it is not necessary to pass
x
explicitly to
each of these procedures. Instead, we allow
x
to be a
free
variable in the internal definitions, as shown below. Then
x
gets its value from the argument with which the enclosing
procedure
sqrt
is called. This discipline is called
lexical
scoping
.
27
(define (sqrt x)
(define (good-enough? guess)
(< (abs (- (square guess) x)) 0.001))
(define (improve guess)
(average guess (/ x guess)))
(define (sqrt-iter guess)
(if (good-enough? guess)
guess
(sqrt-iter (improve guess))))
(sqrt-iter 1.0))
We will use block structure extensively to help us break
up large programs into tractable pieces.
28
The idea of block structure originated with the
programming language
Algol 60. It appears in most advanced
programming languages and is an important tool for helping to organize
the construction of large programs.
4
The
characterization of numbers as “simple data” is a barefaced bluff.
In fact, the treatment of numbers is one of the trickiest and most
confusing aspects of any programming language. Some typical issues
involved are these:
Some computer systems distinguish
integers
, such as 2, from
real numbers
, such as 2.71. Is the real number 2.00 different
from the integer 2?
Are the arithmetic operations used
for integers the same as the operations used for real numbers? Does 6
divided by 2 produce 3, or 3.0? How large a number can we represent?
How many decimal places of accuracy can we represent? Is the range of
integers the same as the range of real numbers?
Above and beyond
these questions, of course, lies a collection of issues concerning
roundoff and truncation errors – the entire science of numerical
analysis. Since our focus in this book is on large-scale program
design rather than on numerical techniques, we are going to ignore
these problems. The numerical examples in this chapter will exhibit
the usual roundoff behavior that one observes when using arithmetic
operations that preserve a limited number of decimal places of
accuracy in noninteger operations.
5
Throughout this book,
when we wish to emphasize the distinction between the input typed by
the user and the response printed by the interpreter, we will show the
latter in slanted characters.
6
Lisp systems typically provide
features to aid the user in formatting expressions. Two especially
useful features are one that automatically indents to the proper
pretty-print position whenever a new line is started and one that
highlights the matching left parenthesis whenever a right parenthesis
is typed.
7
Lisp obeys the convention that every
expression has a value. This convention, together with the old
reputation of Lisp as an inefficient language, is the source of the
quip by Alan Perlis (paraphrasing Oscar Wilde)
that “Lisp programmers know the value of
everything but the cost of nothing.”
8
In this book, we do not show the interpreter's response to
evaluating definitions, since this is highly
implementation-dependent.
9
Chapter 3 will show that this notion of
environment is crucial, both for understanding how the interpreter
works and for implementing interpreters.
10
It may seem strange that the evaluation rule says, as
part of the first step, that we should evaluate the leftmost element
of a combination, since at this point that can only be an operator
such as
+
or
*
representing a built-in primitive procedure such as addition or
multiplication. We will see later that it is useful to be able to work with
combinations whose operators are themselves compound expressions.
11
Special syntactic forms that are simply convenient
alternative surface structures for things that can be written in more
uniform ways are sometimes called
syntactic sugar
, to use a
phrase coined by Peter Landin. In comparison with users of other
languages, Lisp programmers, as a rule, are less concerned with
matters of syntax. (By contrast, examine any Pascal manual and notice
how much of it is devoted to descriptions of syntax.) This disdain
for syntax is due partly to the flexibility of Lisp, which makes it
easy to change surface syntax, and partly to the observation that many
“convenient” syntactic constructs, which make the language less
uniform, end up causing more trouble than they are worth when programs
become large and complex. In the words of Alan Perlis, “Syntactic
sugar causes cancer of the semicolon.”
12
Observe that there are two different operations
being combined here: we are creating the procedure, and we are giving
it the name
square
. It is possible, indeed important, to be
able to separate these two notions – to create procedures without
naming them, and to give names to procedures that have already been
created. We will see how to do this in section
1.3.2
.
13
Throughout this book, we will
describe the general syntax of expressions by using italic symbols
delimited by angle brackets – e.g., <
name
> – to denote the
“slots” in the expression to be filled in when such an expression is
actually used.
14
More
generally, the body of the procedure can be a sequence of expressions.
In this case, the interpreter evaluates each expression in the
sequence in turn and returns the value of the final expression as the
value of the procedure application.
15
Despite the
simplicity of the substitution idea, it turns out to be surprisingly
complicated to give a rigorous mathematical definition of the
substitution process. The problem arises from the possibility of
confusion between the names used for the formal parameters of a
procedure and the (possibly identical) names used in the expressions
to which the procedure may be applied. Indeed, there is a long
history of erroneous definitions of
substitution
in the
literature of logic and programming semantics.
See Stoy 1977 for a
careful discussion of substitution.
16
In
chapter 3 we will introduce
stream processing
, which is a way of
handling apparently “infinite” data structures by incorporating a
limited form of normal-order evaluation. In
section
4.2
we will modify the Scheme
interpreter to produce a normal-order variant of Scheme.
17
“Interpreted as either true or false”
means this: In Scheme, there are two distinguished values that are
denoted by the constants
#t
and
#f
. When the interpreter
checks a predicate's value, it interprets
#f
as false. Any other value
is treated as true. (Thus, providing
#t
is logically
unnecessary, but it is convenient.) In this book we will use
names
true
and
false
, which are associated
with the values
#t
and
#f
respectively.
18
Abs
also uses
the “minus” operator
-
, which, when used with a single
operand, as in
(- x)
, indicates negation.
19
A minor difference
between
if
and
cond
is that the
<
e
> part of each
cond
clause may be a sequence of expressions.
If the corresponding <
p
> is found to be true, the expressions
<
e
> are evaluated in sequence and the value of the final
expression in the sequence is returned as the value of the
cond
.
In an
if
expression, however, the <
consequent
> and
<
alternative
> must be single expressions.
20
Declarative and
imperative descriptions are intimately related, as indeed are
mathematics and computer science. For instance, to say that the
answer produced by a program is
“correct” is to make a declarative
statement about the program. There is a large amount of research
aimed at establishing techniques for
proving that programs are
correct, and much of the technical difficulty of this subject has to
do with negotiating the transition between imperative statements (from
which programs are constructed) and declarative statements (which can
be used to deduce things). In a related vein, an important current
area in programming-language design is the exploration of so-called
very high-level languages, in which one actually programs in terms of
declarative statements. The idea is to make interpreters
sophisticated enough so that, given “what is” knowledge specified by
the programmer, they can generate “how to” knowledge automatically.
This cannot be done in general, but there are important areas where
progress has been made. We shall revisit this idea in chapter 4.
21
This square-root algorithm is actually a special case
of Newton's method, which is a general technique for finding roots of
equations. The square-root algorithm itself was developed by Heron of
Alexandria in the first century
A
.
D
. We will see how to express
the general Newton's method as a Lisp procedure in
section
1.3.4
.
22
We will usually give
predicates names ending with question marks, to help us
remember that they are predicates. This
is just a stylistic convention. As far as the interpreter is
concerned, the question mark is just an ordinary character.
23
Observe that we express our initial guess as 1.0 rather than
1. This would not make any difference in many Lisp implementations.
MIT Scheme, however, distinguishes between exact integers and decimal
values, and dividing two integers produces a rational number rather
than a decimal. For example, dividing 10 by 6 yields 5/3, while
dividing 10.0 by 6.0 yields 1.6666666666666667. (We will learn how to
implement arithmetic on rational numbers in
section
2.1.1
.) If we start with an initial guess of 1
in our square-root program, and
x
is an exact integer, all
subsequent values produced in the square-root computation will be
rational numbers rather than decimals. Mixed operations on rational
numbers and decimals always yield decimals, so starting with an
initial guess of 1.0 forces all subsequent values to be decimals.
24
Readers who are worried about the efficiency
issues involved in using procedure calls to implement iteration should
note the remarks on “tail recursion” in
section
1.2.1
.
25
It is not even clear which of these procedures is a
more efficient implementation. This depends upon the hardware
available. There are machines for which the “obvious”
implementation is the less efficient one. Consider a machine that has
extensive tables of logarithms and antilogarithms stored in a very
efficient manner.
26
The
concept of consistent renaming is actually subtle and difficult to
define formally. Famous logicians have made embarrassing errors
here.
27
Lexical
scoping dictates that free variables in a procedure are taken to refer to
bindings made by enclosing procedure definitions;
that is, they are looked up in
the environment in which the procedure was defined. We will see how
this works in detail in chapter 3 when we study environments and the
detailed behavior of the interpreter.
28
Embedded definitions
must come first in a procedure body. The management is not responsible
for the consequences of running programs that intertwine definition
and use.