Structure and Interpretation of Computer Programs (6 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

- (and <
e
1
>
...
<
e
n
>)The interpreter
evaluates the expressions <
e
> one at a time, in left-to-right order. If
any <
e
> evaluates to false, the value of the
and
expression is false, and the rest of the <
e
>'s are not evaluated.
If all <
e
>'s evaluate to true values, the value of the
and
expression is the value of the last one. - (or <
e
1
>
...
<
e
n
>)The interpreter
evaluates the expressions <
e
> one at a time, in left-to-right order. If
any <
e
> evaluates to a true value, that value is
returned as the value of the
or
expression,
and the rest of the <
e
>'s are not evaluated.
If all <
e
>'s evaluate to false,
the value of the
or
expression is false. - (not <
e
>)The value of a
not
expression is true
when the expression <
e
> evaluates to false, and false otherwise.
Notice that
and
and
or
are special forms, not procedures,
because the subexpressions are not necessarily all evaluated.
Not
is an ordinary procedure.
As an example of how these are used, the condition that a number
x
be in the range 5 <
x
< 10 may be expressed as
(and (> x 5) (< x 10))
As another example, we can define a predicate to test whether one
number is greater than or equal to another as
(define (>= x y)
(or (> x y) (= x y)))
or alternatively as
(define (>= x y)
(not (< x y)))
Exercise 1.1.
Below is a sequence of expressions.
What is the result printed by the interpreter in response to each
expression? Assume that the sequence is to be evaluated in the order
in which it is presented.
10
(+ 5 3 4)
(- 9 1)
(/ 6 2)
(+ (* 2 4) (- 4 6))
(define a 3)
(define b (+ a 1))
(+ a b (* a b))
(= a b)
(if (and (> b a) (< b (* a b)))
b
a)
(cond ((= a 4) 6)
((= b 4) (+ 6 7 a))
(else 25))
(+ 2 (if (> b a) b a))
(* (cond ((> a b) a)
((< a b) b)
(else -1))
(+ a 1))
Exercise 1.2.
Translate the following expression into prefix form
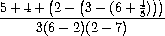
Exercise 1.3.
Define a procedure that takes three numbers as arguments and returns
the sum of the squares of the two larger numbers.
Exercise 1.4.
Observe that our model of evaluation allows for combinations whose
operators are compound expressions. Use this observation to
describe the behavior of the following procedure:
(define (a-plus-abs-b a b)
((if (> b 0) + -) a b))
Exercise 1.5.
Ben Bitdiddle has invented a test to determine whether the interpreter
he is faced with is using applicative-order evaluation or normal-order
evaluation. He defines the following two procedures:
(define (p) (p))
(define (test x y)
(if (= x 0)
0
y))
Then he evaluates the expression
(test 0 (p))
What behavior will Ben observe with an interpreter that uses
applicative-order evaluation? What behavior will he observe with an
interpreter that uses normal-order evaluation? Explain your answer.
(Assume that the evaluation rule for the special form
if
is the
same whether the interpreter is using normal or applicative order:
The predicate expression is evaluated first, and the result
determines whether to evaluate
the consequent or the alternative expression.)
Procedures, as introduced above, are much like ordinary mathematical
functions. They specify a value that is determined by one or more
parameters. But there is an important difference between
mathematical functions and computer procedures. Procedures must be
effective.
As a case in point, consider the problem of computing square
roots. We can define the square-root function as
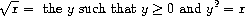
This describes a perfectly legitimate mathematical function. We could
use it to recognize whether one number is the square root of another, or
to derive facts about square roots in general. On the other hand, the
definition does not describe a procedure. Indeed, it tells us almost
nothing about how to actually find the square root of a given number. It
will not help matters to rephrase this definition in pseudo-Lisp:
(define (sqrt x)
(the y (and (>= y 0)
(= (square y) x))))
This only begs the question.
The contrast between function and procedure is a reflection of the
general distinction between describing properties of things and
describing how to do things, or, as it is sometimes referred to, the
distinction between
declarative knowledge and imperative knowledge.
In
mathematics we are usually concerned with declarative (what is)
descriptions, whereas in computer science we are usually concerned
with imperative (how to) descriptions.
20
How does one compute square roots? The most common way is to use
Newton's method of successive approximations, which says that whenever
we have a guess
y
for the value of the square root of a number
x
,
we can perform a simple manipulation to get a better guess (one closer
to the actual square root) by averaging
y
with
x
/
y
.
21
For example, we can compute
the square root of 2 as follows. Suppose our initial guess is 1:
| Guess | Quotient | Average |
| | ||
| 1 | (2/1) = 2 | ((2 + 1)/2) = 1.5 |
| | ||
| 1.5 | (2/1.5) = 1.3333 | ((1.3333 + 1.5)/2) = 1.4167 |
| | ||
| 1.4167 | (2/1.4167) = 1.4118 | ((1.4167 + 1.4118)/2) = 1.4142 |
| | ||
| 1.4142 | ... | ... |
Continuing this process, we obtain better and better
approximations to the square root.
Now let's formalize the process in terms of procedures. We start with
a value for the
radicand (the number whose square root we are trying
to compute) and a value for the guess. If the guess is good enough
for our purposes, we are done; if not, we must repeat the process with an
improved guess. We write this basic strategy as a procedure:
(define (sqrt-iter guess x)
(if (good-enough? guess x)
guess
(sqrt-iter (improve guess x)
x)))
A guess is improved by averaging
it with the quotient of the radicand and the old guess:
(define (improve guess x)
(average guess (/ x guess)))
where
(define (average x y)
(/ (+ x y) 2))
We also have to say what we mean by “good enough.” The
following will do for illustration, but it is not really a very good
test. (See exercise
1.7
.)
The idea is to improve the answer until it is close enough so that its
square differs from the radicand by less than a predetermined
tolerance (here 0.001):
22
(define (good-enough? guess x)
(< (abs (- (square guess) x)) 0.001))
Finally, we need a way to get started. For instance, we can
always guess that the square root of any number is 1:
23
(define (sqrt x)
(sqrt-iter 1.0 x))
If we type these definitions to the interpreter, we can use
sqrt
just as we can use any procedure:
(sqrt 9)
3.00009155413138
(sqrt (+ 100 37))
11.704699917758145
(sqrt (+ (sqrt 2) (sqrt 3)))
1.7739279023207892
(square (sqrt 1000))
1000.000369924366
The
sqrt
program also illustrates that the simple procedural
language we have introduced so far is sufficient for writing any
purely numerical program that one could write in, say, C or
Pascal. This might seem surprising, since we have not included in
our language any iterative
(looping) constructs that direct the
computer to do something over and over again.
Sqrt-iter
, on the
other hand, demonstrates how iteration can be accomplished using no
special construct other than the ordinary ability to call a
procedure.
24
Exercise 1.6.
Alyssa P. Hacker doesn't see why
if
needs
to be provided as a special form. “Why can't I just define it as an
ordinary procedure in terms of
cond
?” she asks.
Alyssa's friend Eva Lu Ator claims this can indeed be done, and
she defines a new version of
if
:
(define (new-if predicate then-clause else-clause)
(cond (predicate then-clause)
(else else-clause)))
Eva demonstrates the program for Alyssa:
(new-if (= 2 3) 0 5)
5
(new-if (= 1 1) 0 5)
0
Delighted, Alyssa uses
new-if
to rewrite the square-root
program:
(define (sqrt-iter guess x)
(new-if (good-enough? guess x)
guess
(sqrt-iter (improve guess x)
x)))
What happens when Alyssa attempts to use this to compute square roots?
Explain.
Exercise 1.7.
The
good-enough?
test used in computing square roots will not be
very effective for finding the square roots of very small numbers.
Also, in real computers, arithmetic operations are almost always
performed with limited precision. This makes our test inadequate for
very large numbers. Explain these statements, with examples showing
how the test fails for small and large numbers. An alternative
strategy for implementing
good-enough?
is to watch how
guess
changes from one iteration to the next and to stop when the
change is a very small fraction of the guess. Design a square-root
procedure that uses this kind of end test. Does this work better for
small and large numbers?
Exercise 1.8.
Newton's method for cube roots is based on the fact that if
y
is an
approximation to the cube root of
x
, then a better approximation is
given by the value

Use this formula to implement a cube-root procedure analogous to the
square-root procedure. (In section
1.3.4
we
will see how to implement Newton's method in general as an abstraction
of these square-root and cube-root procedures.)