Structure and Interpretation of Computer Programs (64 page)

Exercise 3.58.
  Give an interpretation of the stream computed by the following
procedure:

(define (expand num den radix)
  (cons-stream
   (quotient (* num radix) den)
   (expand (remainder (* num radix) den) den radix)))

(
Quotient
is a primitive that returns the integer quotient of
two integers.) What are the successive elements produced by
(expand 1 7 10)
? What is produced by
(expand 3 8 10)
?

Exercise 3.59.
  
In section 
2.5.3
we saw how to implement a
polynomial arithmetic system representing polynomials as lists of
terms. In a similar way, we can work with
power series
, such as

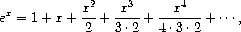
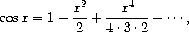
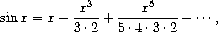
represented as infinite streams.
We will represent the series
a
₀
+
a
₁
x
+
a
₂
x
²
+
a
₃
x
³
+
···
as the stream whose elements are the coefficients
a
₀
,
a
₁
,
a
₂
,
a
₃
,
...
.

a. The integral of the series
a
₀
+
a
₁
x
+
a
₂
x
²
+
a
₃
x
³
+
···
is the series

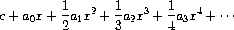
where
c
is any constant.
Define a procedure
integrate-series
that takes as input a stream
a
₀
,
a
₁
,
a
₂
,
...
representing a power series and returns the stream
a
₀
, (1/2)
a
₁
, (1/3)
a
₂
,
...
of coefficients of
the non-constant terms of the integral of the series.
(Since the result has no constant term, it doesn't represent a power
series; when we use
integrate-series
, we will
cons
on
the appropriate constant.)

b. The function
x
⟼
e
^x
is its own
derivative. This implies that
e
^x
and the integral of
e
^x
are the
same series, except for the constant term, which is
e
⁰
= 1.
Accordingly, we can generate the series for
e
^x
as

(define exp-series
  (cons-stream 1 (integrate-series exp-series)))

Show how to generate the series for sine and cosine, starting from the facts
that the derivative of sine is cosine and the derivative of cosine is
the negative of sine:

(define cosine-series
  (cons-stream 1 <
??
>))
(define sine-series
  (cons-stream 0 <
??
>))

Exercise 3.60.
  
With power series represented as streams of coefficients as in
exercise 
3.59
, adding series is implemented by
add-streams
. Complete the definition of the following procedure for
multiplying series:

(define (mul-series s1 s2)
  (cons-stream <
??
> (add-streams <
??
> <
??
>)))

You can test your procedure by verifying that
s
i
n
²
x
+
c
o
s
²
x
= 1, using the series from exercise 
3.59
.

Exercise 3.61.
  Let
S
be a power series (exercise 
3.59
)
whose constant term is 1. Suppose we want
to find the power series 1/
S
, that is, the series
X
such that
S
·
X
= 1. Write
S
= 1 +
S
_R
where
S
_R
is the part of
S
after
the constant term. Then we can solve for
X
as follows:

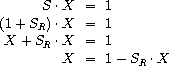
In other words,
X
is the power series whose constant term is 1 and
whose higher-order terms are given by the negative of
S
_R
times
X
.
Use this idea to write a procedure
invert-unit-series
that computes 1/
S
for a power series
S
with
constant term 1.
You will need to use
mul-series
from exercise 
3.60
.

Exercise 3.62.
  
Use the results of exercises 
3.60
and 
3.61
to define a procedure
div-series
that divides two power series.
Div-series
should work for any
two series, provided that the denominator series begins with a
nonzero constant term. (If the denominator has a zero constant term,
then
div-series
should signal an error.)
Show how to use
div-series
together with the result of exercise 
3.59
to generate
the power series for tangent.

Streams with delayed evaluation can be a powerful modeling tool,
providing many of the benefits of local state and assignment.
Moreover, they avoid some of the theoretical tangles that accompany
the introduction of assignment into a programming language.

The stream approach can be illuminating because it allows us to build
systems with different module boundaries than systems organized around
assignment to state variables. For example, we can think of an entire
time series (or signal) as a focus of interest, rather than the values
of the state variables at individual moments. This makes it
convenient to combine and compare components of state from different
moments.

In section 
1.2.1
, we introduced iterative
processes, which proceed by updating state variables. We know now
that we can represent state as a “timeless” stream of values rather
than as a set of variables to be updated. Let's adopt this
perspective in revisiting the square-root procedure from
section 
1.1.7
. Recall that the idea is to generate a
sequence of better and better guesses for the square root of
x
by
applying over and over again the procedure that improves guesses:

(define (sqrt-improve guess x)
  (average guess (/ x guess)))

In our original
sqrt
procedure, we made these guesses be the
successive values of a state variable. Instead we can generate the
infinite stream of guesses, starting with an initial guess of 1:
⁶⁵

(define (sqrt-stream x)
  (define guesses
    (cons-stream 1.0
                 (stream-map (lambda (guess)
                               (sqrt-improve guess x))
                             guesses)))
  guesses)
(display-stream (sqrt-stream 2))
1.
1.5
1.4166666666666665
1.4142156862745097
1.4142135623746899
...

We can generate more and more terms of the stream to get better and
better guesses. If we like, we can write a procedure that keeps
generating terms until the answer is good enough. (See
exercise 
3.64
.)

Another iteration that we can treat in the same way is to generate an
approximation to π, based upon the alternating series that we saw
in section 
1.3.1
:

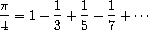
We first generate the stream of summands of the series (the reciprocals
of the odd integers, with alternating signs). Then we take the stream
of sums of more and more terms (using the
partial-sums
procedure
of exercise 
3.55
) and scale the result by 4:

(define (pi-summands n)
  (cons-stream (/ 1.0 n)
               (stream-map - (pi-summands (+ n 2)))))
(define pi-stream
  (scale-stream (partial-sums (pi-summands 1)) 4))
(display-stream pi-stream)
4.
2.666666666666667
3.466666666666667
2.8952380952380956
3.3396825396825403
2.9760461760461765
3.2837384837384844
3.017071817071818
...