Structure and Interpretation of Computer Programs (30 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

29
Rotate90
is a pure rotation only for square
frames, because it also stretches and shrinks the image to fit into
the rotated frame.
30
The diamond-shaped images in figures
2.10
and
2.11
were created with
squash-inwards
applied to
wave
and
rogers
.
All the compound data objects we have used so far were constructed
ultimately from numbers. In this section we extend the representational
capability of our language by introducing the ability to work with
arbitrary symbols as data.
If we can form compound data using symbols, we can have lists such as
(a b c d)
(23 45 17)
((Norah 12) (Molly 9) (Anna 7) (Lauren 6) (Charlotte 4))
Lists containing symbols can look just like the expressions of our
language:
(* (+ 23 45) (+ x 9))
(define (fact n) (if (= n 1) 1 (* n (fact (- n 1)))))
In order to manipulate symbols we need a new element in our language:
the ability to
quote
a data object. Suppose we want to
construct the list
(a b)
. We can't accomplish this with
(list a b)
, because this expression constructs
a list of the
values
of
a
and
b
rather than
the symbols themselves. This issue is well known in the context of
natural languages, where words and sentences may be regarded either as
semantic entities or as character strings (syntactic entities). The
common practice in natural languages is to use quotation marks to
indicate that a word or a sentence is to be treated literally as a
string of characters. For instance, the first letter of “John” is
clearly “J.” If we tell somebody “say your name aloud,” we expect
to hear that person's name. However, if we tell somebody “say `your
name' aloud,” we expect to hear the words “your name.” Note that
we are forced to nest quotation marks to describe what somebody else
might say.
32
We can follow this same practice to identify lists and symbols that are
to be treated as data objects rather than as expressions to be
evaluated. However, our format for quoting differs from that of
natural languages in that we place a quotation mark (traditionally,
the single
quote symbol
'
) only at the beginning of the object
to be quoted. We can get away with this in Scheme syntax because we
rely on blanks and parentheses to delimit objects. Thus, the meaning
of the single quote character is to quote the next object.
33
Now we can distinguish between symbols and their values:
(define a 1)
(define b 2)
(list a b)
(1 2)
(list 'a 'b)
(a b)
(list 'a b)
(a 2)
Quotation also allows us to type in compound objects, using the
conventional printed representation for lists:
34
(car '(a b c))
a
(cdr '(a b c))
(b c)
In keeping with this, we can obtain the empty list by evaluating
'()
, and thus dispense with the variable
nil
.
One additional primitive used in manipulating symbols is
eq?
,
which takes two symbols as arguments and tests whether they are the
same.
35
Using
eq?
,
we can implement a useful procedure called
memq
. This takes two
arguments, a symbol and a list. If the symbol is not contained in the
list (i.e., is not
eq?
to any item in the list), then
memq
returns false. Otherwise, it returns the sublist of
the list beginning with the first occurrence of the symbol:
(define (memq item x)
(cond ((null? x) false)
((eq? item (car x)) x)
(else (memq item (cdr x)))))
For example, the value of
(memq 'apple '(pear banana prune))
is false, whereas the value of
(memq 'apple '(x (apple sauce) y apple pear))
is
(apple pear)
.
Exercise 2.53.
What would the interpreter print in response to evaluating each of the
following expressions?
(list 'a 'b 'c)
(list (list 'george))
(cdr '((x1 x2) (y1 y2)))
(cadr '((x1 x2) (y1 y2)))
(pair? (car '(a short list)))
(memq 'red '((red shoes) (blue socks)))
(memq 'red '(red shoes blue socks))
Exercise 2.54.
Two lists are said to be
equal?
if they contain equal elements
arranged in the same order. For example,
(equal? '(this is a list) '(this is a list))
is true, but
(equal? '(this is a list) '(this (is a) list))
is false. To be more precise, we can define
equal?
recursively in terms of the basic
eq?
equality of symbols by
saying that
a
and
b
are
equal?
if they are both
symbols and the symbols are
eq?
, or if they are both lists such
that
(car a)
is
equal?
to
(car b)
and
(cdr
a)
is
equal?
to
(cdr b)
. Using this idea, implement
equal?
as a procedure.
36
Exercise 2.55.
Eva Lu Ator types to the interpreter the expression
(car ”abracadabra)
To her surprise, the interpreter prints back
quote
. Explain.
As an illustration of symbol manipulation and a further illustration
of data abstraction, consider the design of a procedure that performs
symbolic differentiation of algebraic expressions. We would like the
procedure to take as arguments an algebraic expression and a variable
and to return the derivative of the expression with respect to the
variable. For example, if the arguments to the procedure are
a
x
2
+
b
x
+
c
and
x
, the procedure should return 2
a
x
+
b
. Symbolic
differentiation is of special historical significance in Lisp. It was
one of the motivating examples behind the development of a computer
language for symbol manipulation. Furthermore, it marked the
beginning of the line of research that led to the development of
powerful systems for symbolic mathematical work, which are currently
being used by a growing number of applied mathematicians and
physicists.
In developing the symbolic-differentiation program, we will follow the
same strategy of data abstraction that we followed in developing the
rational-number system of section
2.1.1
. That is, we will first
define a differentiation algorithm that operates on abstract
objects such as “sums,” “products,” and “variables” without
worrying about how these are to be represented. Only afterward will
we address the representation problem.
In order to keep things simple, we will consider a very simple
symbolic-differentiation program that handles expressions that are
built up using only the operations of addition and multiplication with
two arguments. Differentiation of any such expression can be carried
out by applying the following reduction rules:
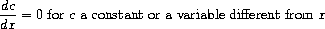
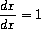
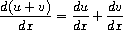
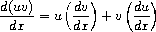
Observe that the latter two rules are recursive in nature. That is,
to obtain the derivative of a sum we first find the derivatives of the
terms and add them. Each of the terms may in turn be an
expression that needs to be decomposed. Decomposing into smaller and
smaller pieces will eventually produce pieces that are either
constants or variables, whose derivatives will be either 0 or 1.
To embody these rules in a procedure we indulge in a little
wishful
thinking, as we did in designing the rational-number implementation.
If we had a means for representing algebraic expressions, we should be
able to tell whether an expression is a sum, a product, a constant, or
a variable. We should be able to extract the parts of an expression.
For a sum, for example we want to be able to extract the addend
(first term) and the augend (second term). We should also be able to
construct expressions from parts. Let us assume that we already have
procedures to implement the following selectors, constructors, and
predicates:
| (variable? e) | Is e a variable? |
| (same-variable? v1 v2) | Are v1 and v2 the same variable? |
(sum? e) | Is e a sum? |
| (addend e) | Addend of the sum e . |
| (augend e) | Augend of the sum e . |
| (make-sum a1 a2) | Construct the sum of a1 and a2 . |
(product? e) | Is e a product? |
| (multiplier e) | Multiplier of the product e . |
| (multiplicand e) | Multiplicand of the product e . |
| (make-product m1 m2) | Construct the product of m1 and m2 . |
number?
,
which identifies numbers, we can express the differentiation rules as the
following procedure:
(define (deriv exp var)
(cond ((number? exp) 0)
((variable? exp)
(if (same-variable? exp var) 1 0))
((sum? exp)
(make-sum (deriv (addend exp) var)
(deriv (augend exp) var)))
((product? exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(else
(error "unknown expression type -- DERIV" exp))))