Structure and Interpretation of Computer Programs (13 page)

We have seen that procedures are, in effect, abstractions that describe
compound operations on numbers independent of the particular numbers.
For example, when we

(define (cube x) (* x x x))

we are not talking about the cube of a particular number, but rather
about a method for obtaining the cube of any number. Of course we
could get along without ever defining this procedure, by
always writing expressions such as

(* 3 3 3)
(* x x x)
(* y y y)        

and never mentioning
cube
explicitly. This would place us at a
serious disadvantage, forcing us to work always at the level of the
particular operations that happen to be primitives in the language
(multiplication, in this case) rather than in terms of higher-level
operations. Our programs would be able to compute cubes, but our
language would lack the ability to express the concept of cubing. One
of the things we should demand from a powerful programming language is
the ability to build abstractions by assigning names to common
patterns and then to work in terms of the abstractions directly.
Procedures provide this ability. This is why all but the most
primitive programming languages include mechanisms for defining
procedures.

Yet even in numerical processing we will be severely limited in our
ability to create abstractions if we are restricted to procedures
whose parameters must be numbers. Often the same programming pattern
will be used with a number of different procedures. To express such
patterns as concepts, we will need to construct procedures that can
accept procedures as arguments or return procedures as values.
Procedures that manipulate procedures are called
higher-order
procedures
. This section shows how higher-order procedures can serve
as powerful abstraction mechanisms, vastly increasing the expressive
power of our language.

Consider the following three procedures. The first computes the sum
of the integers from
a
through
b
:

(define (sum-integers a b)
  (if (> a b)
      0
      (+ a (sum-integers (+ a 1) b))))

The second computes the sum of the cubes of the integers in the given range:

(define (sum-cubes a b)
  (if (> a b)
      0
      (+ (cube a) (sum-cubes (+ a 1) b))))

The third computes the sum of a sequence of terms in the
series

which converges to π/8 (very slowly):
⁴⁹

(define (pi-sum a b)
  (if (> a b)
      0
      (+ (/ 1.0 (* a (+ a 2))) (pi-sum (+ a 4) b))))

These three procedures clearly share a common underlying pattern.
They are for the most part identical, differing only in the name of
the procedure, the function of
a
used to compute the term to be added,
and the function that provides the next value of
a
. We could generate
each of the procedures by filling in slots in the same template:

(define (<
name
> a b)
  (if (> a b)
      0
      (+ (<
term
> a)
         (<
name
> (<
next
> a) b))))

The presence of such a common pattern is strong evidence that there is
a useful abstraction waiting to be brought to the surface. Indeed,
mathematicians long ago identified the abstraction of
summation of a series
and invented “sigma
notation,” for example

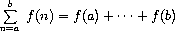
to express this concept. The power of sigma notation is that it
allows mathematicians to deal with the concept of summation
itself rather than only with particular sums – for example, to
formulate general results about sums that are independent of the
particular series being summed.

Similarly, as program designers, we would like our language to
be powerful enough so that we can write a procedure that expresses the
concept of summation itself rather than only procedures
that compute particular sums. We can do so readily in our
procedural language by taking the common template shown above and
transforming the “slots” into formal parameters:

(define (sum term a next b)
  (if (> a b)
      0
      (+ (term a)
         (sum term (next a) next b))))

Notice that
sum
takes as its arguments the lower and upper bounds
a
 and 
b
together with the procedures
term
and
next
.
We can use
sum
just as we would any procedure. For example, we can
use it (along with a procedure
inc
that increments its argument by 1)
to define
sum-cubes
:

(define (inc n) (+ n 1))
(define (sum-cubes a b)
  (sum cube a inc b))

Using this, we can compute the sum of the cubes of the integers from 1
to 10:

(sum-cubes 1 10)
3025

With the aid of an identity procedure to compute the term, we can define
sum-integers
in terms of
sum
:

(define (identity x) x)
(define (sum-integers a b)
  (sum identity a inc b))

Then we can add up the integers from 1 to 10:

(sum-integers 1 10)
55

We can also define
pi-sum
in the same way:
⁵⁰

(define (pi-sum a b)
  (define (pi-term x)
    (/ 1.0 (* x (+ x 2))))
  (define (pi-next x)
    (+ x 4))
  (sum pi-term a pi-next b))

Using these procedures, we can compute an approximation to
π:

(* 8 (pi-sum 1 1000))
3.139592655589783

Once we have
sum
, we can use it as a building block in
formulating further concepts. For instance, the
definite integral of a
function
f
between the limits
a
and
b
can be approximated
numerically using the formula

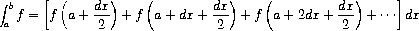
for small values of
d
x
. We can express this directly as a
procedure:

(define (integral f a b dx)
  (define (add-dx x) (+ x dx))
  (* (sum f (+ a (/ dx 2.0)) add-dx b)
     dx))
(integral cube 0 1 0.01)
.24998750000000042
(integral cube 0 1 0.001)
.249999875000001

(The exact value of the integral of
cube
between 0 and 1 is 1/4.)

Exercise 1.29.
  
Simpson's Rule is a more accurate method of numerical integration than
the method illustrated above. Using Simpson's Rule, the integral of a
function
f
between
a
and
b
is approximated as

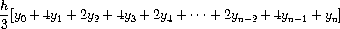
where
h
= (
b
-
a
)/
n
, for some even integer
n
, and
y
_k
=
f
(
a
+
k
h
).
(Increasing
n
increases the accuracy of the approximation.) Define
a procedure that takes as arguments
f
,
a
,
b
, and
n
and returns
the value of the integral, computed using Simpson's Rule.
Use your procedure to integrate
cube
between 0 and 1
(with
n
= 100 and
n
= 1000), and compare the results to those of the
integral
procedure shown above.

Exercise 1.30.
  
The
sum
procedure above generates a linear recursion. The
procedure can be rewritten so that the sum is performed iteratively.
Show how to do this by filling in the missing expressions in the
following definition:

(define (sum term a next b)
  (define (iter a result)
    (if <
??
>
        <
??
>
        (iter <
??
> <
??
>)))
  (iter <
??
> <
??
>))

Exercise 1.31.
  
a.  The
sum
procedure is only the simplest of a vast number of
similar abstractions that can be captured as higher-order procedures.
⁵¹
Write an analogous procedure
called
product
that returns the product of the values of a
function at points over a given range.
Show how to define
factorial
in terms of
product
. Also use
product
to compute approximations to
π using the formula
⁵²

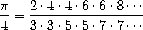
b.  If your
product
procedure generates a recursive process, write one that generates
an iterative process.
If it generates an iterative process, write one that generates
a recursive process.

Exercise 1.32.
  
a. Show that
sum
and
product
(exercise 
1.31
) are both special cases of a still more
general notion called
accumulate
that combines a collection of
terms, using some general accumulation function: