Structure and Interpretation of Computer Programs (25 page)

For example, to compute 1 + 3
x
+ 5
x
³
+
x
⁵
at
x
= 2 you would evaluate

(horner-eval 2 (list 1 3 0 5 0 1))

Exercise 2.35.
  Redefine
count-leaves
from section 
2.2.2
as an
accumulation:

(define (count-leaves t)
  (accumulate <
??
> <
??
> (map <
??
> <
??
>)))

Exercise 2.36.
  The procedure
accumulate-n
is similar to
accumulate
except
that it takes as its third argument a sequence of sequences, which are all
assumed to have the same number of elements. It applies the
designated accumulation procedure to combine all the first elements of
the sequences, all the second elements of the sequences, and so on, and
returns a sequence of the results. For instance, if
s
is a sequence
containing four sequences,
((1 2 3) (4 5 6) (7 8 9) (10 11 12)),
then the value of
(accumulate-n + 0 s)
should be the sequence
(22 26 30)
. Fill in the missing expressions
in the following definition of
accumulate-n
:

(define (accumulate-n op init seqs)
  (if (null? (car seqs))
      nil
      (cons (accumulate op init <
??
>)
            (accumulate-n op init <
??
>))))

Exercise 2.37.
  
Suppose we represent vectors
v
= (
v
_i
) as sequences of numbers, and
matrices
m
= (
m
_i
j
) as sequences of vectors (the rows of the matrix).
For example, the matrix

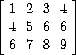
is represented as the sequence
((1 2 3 4) (4 5 6 6) (6 7 8 9))
.
With this representation, we can use sequence operations to concisely
express the basic matrix and vector operations. These operations
(which are described in any book on matrix algebra) are the following:

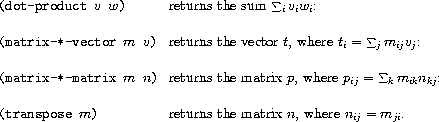
We can define the dot product as
¹⁷

(define (dot-product v w)
  (accumulate + 0 (map * v w)))

Fill in the missing expressions in the following procedures for
computing the other matrix operations. (The procedure
accumulate-n
is
defined in exercise 
2.36
.)

(define (matrix-*-vector m v)
  (map <
??
> m))
(define (transpose mat)
  (accumulate-n <
??
> <
??
> mat))
(define (matrix-*-matrix m n)
  (let ((cols (transpose n)))
    (map <
??
> m)))

Exercise 2.38.
  
The
accumulate
procedure is also known as
fold-right
,
because it combines the first element of the sequence with the result
of combining all the elements to the right. There is also a
fold-left
, which is
similar to
fold-right
, except
that it combines elements working in the opposite direction:

(define (fold-left op initial sequence)
  (define (iter result rest)
    (if (null? rest)
        result
        (iter (op result (car rest))
              (cdr rest))))
  (iter initial sequence))

What are the values of

(fold-right / 1 (list 1 2 3))
(fold-left / 1 (list 1 2 3))
(fold-right list nil (list 1 2 3))
(fold-left list nil (list 1 2 3))

Give a property that
op
should satisfy to guarantee that
fold-right
and
fold-left
will produce the same values for any
sequence.

Exercise 2.39.
  
Complete the following definitions of
reverse
(exercise 
2.18
) in terms of
fold-right
and
fold-left
from exercise 
2.38
:

(define (reverse sequence)
  (fold-right (lambda (x y) <
??
>) nil sequence))
(define (reverse sequence)
  (fold-left (lambda (x y) <
??
>) nil sequence))

We can extend the sequence paradigm to include many
computations that are commonly expressed using nested loops.
¹⁸
Consider
this problem: Given a positive integer
n
, find all ordered pairs of
distinct positive integers
i
and
j
, where 1
<
j
<
i
<
n
, such
that
i
+
j
is prime. For example, if
n
is 6, then the pairs are
the following:

A natural way to organize this computation is to generate the sequence
of all ordered pairs of positive integers less than or equal to
n
,
filter to select those pairs whose sum is prime, and
then, for each pair (
i
,
j
) that passes through the filter, produce the triple
(
i
,
j
,
i
+
j
).

Here is a way to generate the sequence of pairs: For each integer
i
<
n
, enumerate the integers
j
<
i
, and for each such
i
and
j
generate the pair (
i
,
j
). In terms of sequence operations, we map
along the sequence
(enumerate-interval 1 n)
. For each
i
in
this sequence, we map along the sequence
(enumerate-interval 1 (-
i 1))
. For each
j
in this latter sequence, we generate the pair
(list i j)
. This gives us a sequence of pairs for each
i
.
Combining all the sequences for all the
i
(by accumulating with
append
) produces the required sequence of pairs:
¹⁹

(accumulate append
            nil
            (map (lambda (i)
                   (map (lambda (j) (list i j))
                        (enumerate-interval 1 (- i 1))))
                 (enumerate-interval 1 n)))

The combination of mapping and accumulating with
append
is so common in this
sort of program that we will isolate it as a separate procedure:

(define (flatmap proc seq)
  (accumulate append nil (map proc seq)))

Now filter this sequence of pairs to find those whose sum is prime. The
filter predicate is called for each element of the sequence; its
argument is a pair and it must extract the integers from the pair.
Thus, the predicate to apply to each element in the sequence is

(define (prime-sum? pair)
  (prime? (+ (car pair) (cadr pair))))

Finally, generate the sequence of results by mapping over the filtered
pairs using the following procedure, which constructs a triple
consisting of the two elements of the pair along with their sum:

(define (make-pair-sum pair)
  (list (car pair) (cadr pair) (+ (car pair) (cadr pair))))

Combining all these steps yields the complete procedure:

(define (prime-sum-pairs n)
  (map make-pair-sum
       (filter prime-sum?
               (flatmap
                (lambda (i)
                  (map (lambda (j) (list i j))
                       (enumerate-interval 1 (- i 1))))
                (enumerate-interval 1 n)))))

Nested mappings are also useful for sequences other than those that
enumerate intervals. Suppose we wish to generate all the
permutations
of a set
S
; that is, all the ways of ordering the items in
the set. For instance, the permutations of {1,2,3} are
{1,2,3}, { 1,3,2}, {2,1,3}, { 2,3,1}, { 3,1,2}, and
{ 3,2,1}. Here is a plan for generating the permutations of 
S
:
For each item
x
in
S
, recursively generate the sequence of
permutations of
S
-
x
,
²⁰
and adjoin
x
to the front of each one. This yields, for each
x
in
S
, the sequence
of permutations of
S
that begin with 
x
. Combining these
sequences for all
x
gives all the permutations of 
S
:
²¹

(define (permutations s)
  (if (null? s)                    
; empty set?
      (list nil)                   
; sequence containing empty set
      (flatmap (lambda (x)
                 (map (lambda (p) (cons x p))
                      (permutations (remove x s))))
               s)))

Notice how this strategy reduces the problem of generating
permutations of
S
to the problem of generating the permutations of
sets with fewer elements than
S
. In the terminal case, we work our
way down to the empty list, which represents a set of no elements.
For this, we generate
(list nil)
, which is a sequence with one
item, namely the set with no elements. The
remove
procedure
used in
permutations
returns all the items in a given sequence
except for a given item. This can be expressed as a simple filter:

(define (remove item sequence)
  (filter (lambda (x) (not (= x item)))
          sequence))

Exercise 2.40.
  Define a procedure
unique-pairs
that, given an integer
n
,
generates the sequence of pairs (
i
,
j
) with 1
<
j
<
i
<
n
. Use
unique-pairs
to simplify the definition of
prime-sum-pairs
given above.

Exercise 2.41.
  Write a procedure to find all ordered
triples of distinct positive integers
i
,
j
, and 
k
less than or
equal to a given integer
n
that sum to a given integer
s
.

Exercise 2.42.
  

Figure 2.8:
  A solution to the eight-queens puzzle.