Structure and Interpretation of Computer Programs (20 page)

But exactly what is meant by
data
? It is not enough to say
“whatever is implemented by the given selectors and constructors.”
Clearly, not every arbitrary set of three procedures can serve as an
appropriate basis for the rational-number implementation. We need to
guarantee that,
if we construct a rational number
x
from a pair
of integers
n
and
d
, then extracting the
numer
and the
denom
of
x
and dividing them should yield the same result
as dividing
n
by
d
. In other words,
make-rat
,
numer
, and
denom
must satisfy the condition that, for any
integer
n
and any non-zero integer
d
, if
x
is
(
make-rat n d
), then

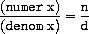
In fact, this is the only condition
make-rat
,
numer
, and
denom
must fulfill in order to form a suitable basis for a
rational-number representation. In general, we can think of data as
defined by some collection of selectors and constructors, together
with specified conditions that these procedures must fulfill in order
to be a valid representation.
⁵

This point of view can serve to define not only “high-level” data
objects, such as rational numbers, but lower-level objects as well.
Consider the notion of a pair, which we used in order to define our
rational numbers. We never actually said what a pair was, only that
the language supplied procedures
cons
,
car
, and
cdr
for operating on pairs. But the only thing we need to know about
these three operations
is that if we glue two objects together using
cons
we can retrieve the objects using
car
and
cdr
.
That is, the operations satisfy the condition that, for any objects
x
and
y
, if
z
is
(cons x y)
then
(car z)
is
x
and
(cdr z)
is
y
. Indeed, we mentioned that
these three procedures are included as primitives in our language.
However, any triple of procedures that satisfies the above condition
can be used as the basis for implementing pairs. This point is
illustrated strikingly by the fact that we could implement
cons
,
car
, and
cdr
without using any data structures at all but
only using procedures. Here are the definitions:

(define (cons x y)
  (define (dispatch m)
    (cond ((= m 0) x)
          ((= m 1) y)
          (else (error "Argument not 0 or 1 -- CONS" m))))
  dispatch)
(define (car z) (z 0))
(define (cdr z) (z 1))

This use of procedures corresponds to nothing like our intuitive
notion of what data should be. Nevertheless, all we need to do to
show that this is a valid way to represent pairs is to verify that
these procedures satisfy the condition given above.

The subtle point to notice is that the value returned by
(cons x
y)
is a procedure – namely the internally defined procedure
dispatch
, which takes one argument and returns either
x
or
y
depending on whether the argument is 0 or 1. Correspondingly,
(car z)
is defined to apply
z
to 0. Hence, if
z
is the
procedure formed by
(cons x y)
, then
z
applied to 0 will
yield
x
. Thus, we have shown that
(car (cons x y))
yields
x
, as desired. Similarly,
(cdr (cons x y))
applies the
procedure returned by
(cons x y)
to 1, which returns
y
.
Therefore, this procedural implementation of pairs is a valid
implementation, and if we access pairs using only
cons
,
car
, and
cdr
we cannot distinguish this implementation from one
that uses “real” data structures.

The point of exhibiting the procedural representation of pairs is not
that our language works this way (Scheme, and Lisp systems in general,
implement pairs directly, for efficiency reasons) but that it could
work this way. The procedural representation, although obscure, is a
perfectly adequate way to represent pairs, since it fulfills the only
conditions that pairs need to fulfill. This example also demonstrates
that the ability to manipulate procedures as objects automatically
provides the ability to represent compound data. This may seem a
curiosity now, but procedural representations of data will play a
central role in our programming repertoire. This style of programming
is often called
message passing
, and we will be using it as a
basic tool in chapter 3 when we address the issues of modeling and
simulation.

Exercise 2.4.
  Here is an alternative procedural representation of pairs. For this
representation, verify that
(car (cons x y))
yields
x
for
any objects
x
and
y
.

(define (cons x y)
  (lambda (m) (m x y)))
(define (car z)
  (z (lambda (p q) p)))

What is the corresponding definition of
cdr
? (Hint: To verify
that this works, make use of the substitution model of
section 
1.1.5
.)

Exercise 2.5.
  Show that we can represent pairs of nonnegative integers using only
numbers and arithmetic operations if we represent the pair
a
and
b
as the integer that is the product 2
^a
3
^b
. Give the corresponding
definitions of the procedures
cons
,
car
, and
cdr
.

Exercise 2.6.
  In case representing pairs as procedures wasn't mind-boggling enough,
consider that, in a language that can manipulate procedures, we can
get by without numbers (at least insofar as nonnegative integers are
concerned) by implementing 0 and the operation of adding 1 as

(define zero (lambda (f) (lambda (x) x)))
(define (add-1 n)
  (lambda (f) (lambda (x) (f ((n f) x)))))

This representation is known as
Church numerals
, after its
inventor,
Alonzo Church, the logician who invented the λ
calculus.

Define
one
and
two
directly (not in terms of
zero
and
add-1
). (Hint: Use substitution to evaluate
(add-1 zero)
).
Give a direct definition of the addition procedure
+
(not in
terms of repeated application of
add-1
).

Alyssa P. Hacker is designing a system to help people solve
engineering problems. One feature she wants to provide in her system
is the ability to manipulate inexact quantities (such as measured
parameters of physical devices) with known precision, so that when
computations are done with such approximate quantities the results
will be numbers of known precision.

Electrical engineers will be using Alyssa's system to compute
electrical quantities. It is sometimes necessary for them to compute
the value of a parallel equivalent resistance
R
_p
of two
resistors
R
₁
and
R
₂
using the formula

Resistance values are usually known only up to some
tolerance
guaranteed by the manufacturer of the resistor. For example, if you
buy a resistor labeled “6.8 ohms with 10% tolerance” you can only
be sure that the resistor has a resistance between 6.8 - 0.68 = 6.12 and
6.8 + 0.68 = 7.48 ohms. Thus, if you have a 6.8-ohm 10% resistor in
parallel with a 4.7-ohm 5% resistor, the resistance of the
combination can range from about 2.58 ohms (if the two resistors are
at the lower bounds) to about 2.97 ohms (if the two resistors are at
the upper bounds).

Alyssa's idea is to implement “interval arithmetic” as a set of
arithmetic operations for combining “intervals” (objects
that represent the range of possible values of an inexact quantity).
The result of adding, subtracting, multiplying, or dividing two
intervals is itself an interval, representing the range of the
result.

Alyssa postulates the existence of an abstract object called an
“interval” that has two endpoints: a lower bound and an upper bound.
She also presumes that, given the endpoints of an interval, she can
construct the interval using the data constructor
make-interval
.
Alyssa first writes a procedure for adding two intervals. She
reasons that the minimum value the sum could be is the sum of the two
lower bounds and the maximum value it could be is the sum of the two
upper bounds:

(define (add-interval x y)
  (make-interval (+ (lower-bound x) (lower-bound y))
                 (+ (upper-bound x) (upper-bound y))))

Alyssa also works out the product of two intervals by finding the
minimum and the maximum of the products of the bounds and using them
as the bounds of the resulting interval. (
Min
and
max
are
primitives that find the minimum or maximum of any number of
arguments.)

(define (mul-interval x y)
  (let ((p1 (* (lower-bound x) (lower-bound y)))
        (p2 (* (lower-bound x) (upper-bound y)))
        (p3 (* (upper-bound x) (lower-bound y)))
        (p4 (* (upper-bound x) (upper-bound y))))
    (make-interval (min p1 p2 p3 p4)
                   (max p1 p2 p3 p4))))

To divide two intervals, Alyssa multiplies the first by the reciprocal of
the second. Note that the bounds of the reciprocal interval are
the reciprocal of the upper bound and the reciprocal of the lower bound, in
that order.

(define (div-interval x y)
  (mul-interval x 
                (make-interval (/ 1.0 (upper-bound y))
                               (/ 1.0 (lower-bound y)))))

Exercise 2.7.
  Alyssa's program is incomplete because she has not specified the
implementation of the interval abstraction. Here is a definition of
the interval constructor:

(define (make-interval a b) (cons a b))

Define selectors
upper-bound
and
lower-bound
to complete
the implementation.

Exercise 2.8.
  Using reasoning analogous to Alyssa's, describe how the difference
of two intervals may be computed. Define a corresponding subtraction
procedure, called
sub-interval
.

Exercise 2.9.
  
The
width
of an interval is half of the difference between its
upper and lower bounds. The width is a measure of the uncertainty of
the number specified by the interval. For some arithmetic operations
the width of the result of combining two intervals is a function only
of the widths of the argument intervals, whereas for others the width
of the combination is not a function of the widths of the argument
intervals. Show that the width of the sum (or difference) of two
intervals is a function only of the widths of the intervals being
added (or subtracted). Give examples to show that this is not true
for multiplication or division.

Exercise 2.10.
  
Ben Bitdiddle, an expert systems programmer, looks over Alyssa's
shoulder and comments that it is not clear what it means to
divide by an interval that spans zero. Modify Alyssa's code to
check for this condition and to signal an error if it occurs.

Exercise 2.11.
  
In passing, Ben also cryptically comments: “By testing the signs of
the endpoints of the intervals, it is possible to break
mul-interval
into nine cases, only one of which requires more than
two multiplications.” Rewrite this procedure using Ben's
suggestion.