Structure and Interpretation of Computer Programs (23 page)

Unfortunately, defining
square-list
this way produces the answer
list in the reverse order of the one desired. Why?

Louis then tries to fix his bug by interchanging the arguments to
cons
:

(define (square-list items)
  (define (iter things answer)
    (if (null? things)
        answer
        (iter (cdr things)
              (cons answer
                    (square (car things))))))
  (iter items nil))

This doesn't work either. Explain.

Exercise 2.23.
  The procedure
for-each
is similar to
map
. It takes as
arguments a procedure and a list of elements. However, rather than
forming a list of the results,
for-each
just applies the procedure
to each of the elements in turn, from left to right. The values
returned by applying the procedure to the elements are not used at
all –
for-each
is used with procedures that perform an action,
such as printing. For example,

(for-each (lambda (x) (newline) (display x))
          (list 57 321 88))
57
321
88

The value returned by the call to
for-each
(not illustrated above)
can be something arbitrary, such as true. Give an
implementation of
for-each
.

The representation of sequences in terms of lists generalizes
naturally to represent sequences whose elements may
themselves be sequences. For example, we can regard the object
((1 2) 3 4)
constructed by

(cons (list 1 2) (list 3 4))

as a list of three items, the first of which is itself a list,
(1 2)
. Indeed, this is suggested by the form in which the result is
printed by the interpreter. Figure 
2.5
shows
the representation of this structure in terms of pairs.

Figure 2.5:
  Structure formed by
(cons (list 1 2) (list 3 4))
.

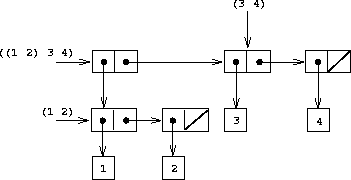Another way to think of sequences whose elements are sequences is as
trees
. The elements of the sequence are the branches of the
tree, and elements that are themselves sequences are subtrees.
Figure 
2.6
shows the structure in
figure 
2.5
viewed as a tree.

Figure 2.6:
  The list structure in figure 
2.5
viewed as a tree.

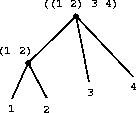Recursion is a natural tool for dealing with tree structures, since
we can often reduce operations on trees to operations on their
branches, which reduce in turn to operations on the branches of the
branches, and so on, until we reach the leaves of the tree.
As an example, compare the
length
procedure of
section 
2.2.1
with the
count-leaves
procedure, which
returns the total number of leaves of a tree:

(define x (cons (list 1 2) (list 3 4)))
(length x)
3
(count-leaves x)
4
(list x x)
(((1 2) 3 4) ((1 2) 3 4))
(length (list x x))
2
(count-leaves (list x x))
8

To implement
count-leaves
, recall the recursive plan for computing
length
:

• Length
  of a list
  x
  is 1 plus
  length
  of the
  cdr
  of
  x
  .
  
• Length
  of the empty list is 0.
  

Count-leaves
is similar. The value for the empty list is the same:

• Count-leaves
  of the empty list is 0.
  

But in the reduction step, where we strip off the
car
of the
list, we must take into account that the
car
may itself be a
tree whose leaves we need to count. Thus, the appropriate reduction
step is

• Count-leaves
  of a tree
  x
  is
  count-leaves
  of the
  car
  of
  x
  plus
  count-leaves
  of the
  cdr
  of
  x
  .
  

Finally, by taking
car
s we reach
actual leaves, so we need another base case:

• Count-leaves
  of a leaf is 1.
  

To aid
in writing recursive procedures on trees, Scheme provides the primitive
predicate
pair?
, which tests whether its argument is a pair.
Here is the complete procedure:
¹³

(define (count-leaves x)
  (cond ((null? x) 0)  
        ((not (pair? x)) 1)
        (else (+ (count-leaves (car x))
                 (count-leaves (cdr x))))))

Exercise 2.24.
  Suppose we evaluate the expression
(list 1 (list 2 (list 3 4)))
.
Give the result printed by the interpreter, the corresponding
box-and-pointer structure, and the interpretation of this as a tree
(as in figure 
2.6
).

Exercise 2.25.
  Give combinations of
car
s and
cdr
s that will pick 7 from
each of the following lists:

(1 3 (5 7) 9)
((7))
(1 (2 (3 (4 (5 (6 7))))))

Exercise 2.26.
  Suppose we define
x
and
y
to be two lists:

(define x (list 1 2 3))
(define y (list 4 5 6))

What result is printed by the interpreter in response to evaluating
each of the following expressions:

(append x y)
(cons x y)
(list x y)

Exercise 2.27.
  Modify your
reverse
procedure of exercise 
2.18
to
produce a
deep-reverse
procedure that takes a list as argument
and returns as its value the list with its elements reversed and with
all sublists deep-reversed as well. For example,

(define x (list (list 1 2) (list 3 4)))
x
((1 2) (3 4))
(reverse x)
((3 4) (1 2))
(deep-reverse x)
((4 3) (2 1))

Exercise 2.28.
  Write a procedure
fringe
that takes as argument a tree
(represented as a list) and returns a list whose elements are all the
leaves of the tree arranged in left-to-right order. For example,

(define x (list (list 1 2) (list 3 4)))
(fringe x)
(1 2 3 4)
(fringe (list x x))
(1 2 3 4 1 2 3 4)

Exercise 2.29.
  
A binary mobile consists of two branches, a left branch and a right
branch. Each branch is a rod of a certain length, from which hangs
either a weight or another binary mobile. We can represent a binary
mobile using compound data by constructing it from two branches (for
example, using
list
):

(define (make-mobile left right)
  (list left right))

A branch is constructed from a
length
(which must be a number)
together with a
structure
, which may be either a number
(representing a simple weight) or another mobile:

(define (make-branch length structure)
  (list length structure))

a.  Write the corresponding selectors
left-branch
and
right-branch
, which return the branches of a mobile, and
branch-length
and
branch-structure
, which return
the components of a branch.

b.  Using your selectors, define a procedure
total-weight
that returns the total weight of a mobile.

c.  A mobile is said to be
balanced
if the torque applied
by its top-left branch is equal to that applied by its top-right
branch (that is, if the length of the left rod multiplied by the
weight hanging from that rod is equal to the corresponding product for
the right side) and if each of the submobiles hanging off its branches
is balanced. Design a predicate that tests whether a binary mobile is
balanced.

d.  Suppose we change the representation of mobiles so that the
constructors are

(define (make-mobile left right)
  (cons left right))
(define (make-branch length structure)
  (cons length structure))

How much do you need to change your programs to convert to the new
representation?

Just as
map
is a powerful abstraction for dealing with sequences,
map
together with recursion is a powerful abstraction for
dealing with trees. For instance, the
scale-tree
procedure, analogous to
scale-list
of
section 
2.2.1
, takes as arguments a numeric factor and a
tree whose leaves are numbers. It returns a tree of the same shape,
where each number is multiplied by the factor.
The recursive plan for
scale-tree
is similar to the one for
count-leaves
:

(define (scale-tree tree factor)
  (cond ((null? tree) nil)
        ((not (pair? tree)) (* tree factor))
        (else (cons (scale-tree (car tree) factor)
                    (scale-tree (cdr tree) factor)))))
(scale-tree (list 1 (list 2 (list 3 4) 5) (list 6 7))
            10)
(10 (20 (30 40) 50) (60 70))

Another way to implement
scale-tree
is to regard the
tree as a sequence of sub-trees and use
map
. We map
over the sequence, scaling each sub-tree in turn, and return the list
of results. In the base case, where the tree is a leaf, we simply
multiply by the factor:

(define (scale-tree tree factor)
  (map (lambda (sub-tree)
         (if (pair? sub-tree)
             (scale-tree sub-tree factor)
             (* sub-tree factor)))
       tree))

Many tree operations can be implemented by similar combinations of
sequence operations and recursion.

Exercise 2.30.
  Define a procedure
square-tree
analogous to the
square-list
procedure of exercise 
2.21
. That is,
square-list
should behave as follows:

(square-tree
 (list 1
       (list 2 (list 3 4) 5)
       (list 6 7)))
(1 (4 (9 16) 25) (36 49))

Define
square-tree
both directly (i.e., without using any
higher-order procedures) and also by using
map
and recursion.

Exercise 2.31.
  Abstract your answer to exercise 
2.30
to produce a
procedure
tree-map
with the property that
square-tree
could be defined as

(define (square-tree tree) (tree-map square tree))

Exercise 2.32.
  We can represent a
set as a list of distinct elements, and we can
represent the set of all subsets of the set as a list of lists. For
example, if the set is
(1 2 3)
, then the set of all subsets is
(() (3) (2) (2 3) (1) (1 3) (1 2) (1 2 3))
. Complete the
following definition of a procedure that generates the set of subsets
of a set and give a clear explanation of why it works:

(define (subsets s)
  (if (null? s)
      (list nil)
      (let ((rest (subsets (cdr s))))
        (append rest (map <
??
> rest)))))

In working with compound data, we've stressed how data abstraction
permits us to design programs without becoming enmeshed in the details
of data representations, and how abstraction preserves for us the
flexibility to experiment with alternative representations. In this
section, we introduce another powerful design principle for working
with data structures – the use of
conventional interfaces
.

In section 
1.3
we saw how program
abstractions, implemented as higher-order procedures, can capture
common patterns in programs that deal with numerical data. Our
ability to formulate analogous operations for working with compound
data depends crucially on the style in which we manipulate our data
structures. Consider, for example, the following procedure, analogous
to the
count-leaves
procedure of section 
2.2.2
, which
takes a tree as argument and computes the sum of the squares of the
leaves that are odd: