Structure and Interpretation of Computer Programs (27 page)

Figure 
2.12
shows the drawing of a painter called
wave4
that is built up in two stages starting from
wave
:

(define wave2 (beside wave (flip-vert wave)))
(define wave4 (below wave2 wave2))

Figure 2.12:
  Creating a complex figure,
starting from the
wave
painter of figure 
2.10
.

(define wave2                         (define wave4   (beside wave (flip-vert wave)))       (below wave2 wave2))

In building up a complex image in this manner we are exploiting the
fact that painters are closed under the language's means of
combination. The
beside
or
below
of two painters is
itself a painter; therefore, we can use it as an element in making
more complex painters. As with building up list structure using
cons
, the closure of our data under the means of combination is
crucial to the ability to create complex structures while using only a
few operations.

Once we can combine painters, we would like to be able to abstract
typical patterns of combining painters.
We will implement the painter operations as Scheme procedures.
This means that we don't need a special abstraction mechanism
in the picture language:
Since the means of combination
are ordinary Scheme procedures, we automatically have the capability
to do anything with painter operations that we can do with
procedures.
For example, we can abstract the pattern in
wave4
as

(define (flipped-pairs painter)
  (let ((painter2 (beside painter (flip-vert painter))))
    (below painter2 painter2)))

and define
wave4
as an instance of this pattern:

(define wave4 (flipped-pairs wave))

We can also define recursive operations.
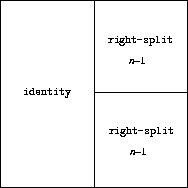
Here's one that makes painters split and branch
towards the right as shown in figures 
2.13
and  
2.14
:

(define (right-split painter n)
  (if (= n 0)
      painter
      (let ((smaller (right-split painter (- n 1))))
        (beside painter (below smaller smaller)))))

Figure 2.13:
  Recursive plans for
right-split
and
corner-split
.

right-split  n                    corner-split  n

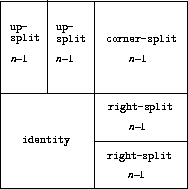
We can produce balanced patterns by branching upwards
as well as towards the right (see exercise 
2.44
and figures 
2.13
and  
2.14
):

(define (corner-split painter n)
  (if (= n 0)
      painter
      (let ((up (up-split painter (- n 1)))
            (right (right-split painter (- n 1))))
        (let ((top-left (beside up up))
              (bottom-right (below right right))
              (corner (corner-split painter (- n 1))))
          (beside (below painter top-left)
                  (below bottom-right corner))))))

Figure 2.14:
  The recursive operations
right-split
and
corner-split
applied to the painters
wave
and
rogers
.
Combining four
corner-split
figures produces
symmetric
square-limit
designs as shown
in figure 
2.9
.

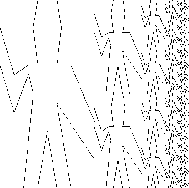(right-split wave 4)         (right-split rogers 4)                  (corner-split wave 4)         (corner-split rogers 4)

By placing four copies of a
corner-split
appropriately, we obtain a pattern called
square-limit
, whose
application to
wave
and
rogers
is shown in
figure 
2.9
:

(define (square-limit painter n)
  (let ((quarter (corner-split painter n)))
    (let ((half (beside (flip-horiz quarter) quarter)))
      (below (flip-vert half) half))))

Exercise 2.44.
  Define the procedure
up-split
used by
corner-split
.
It is similar to
right-split
, except that it switches the
roles of
below
and
beside
.

In addition to abstracting patterns of combining painters, we can work
at a higher level, abstracting patterns of combining painter operations.
That is, we can view the painter operations as elements to manipulate
and can write means of combination for these elements – procedures that
take painter operations as arguments and create new painter operations.

For example,
flipped-pairs
and
square-limit
each
arrange four copies of a painter's image in a square pattern; they differ
only in how they orient the copies.
One way to abstract this pattern of painter combination is with
the following procedure, which takes four one-argument painter operations
and produces a painter operation that transforms a given
painter with those four operations and arranges the results in a square.
Tl
,
tr
,
bl
, and
br
are the
transformations to apply to the top left copy, the top right copy,
the bottom left copy, and the bottom right copy, respectively.

(define (square-of-four tl tr bl br)
  (lambda (painter)
    (let ((top (beside (tl painter) (tr painter)))
          (bottom (beside (bl painter) (br painter))))
      (below bottom top))))

Then
flipped-pairs
can be defined in terms
of
square-of-four
as follows:
²⁴

(define (flipped-pairs painter)
  (let ((combine4 (square-of-four identity flip-vert
                                  identity flip-vert)))
    (combine4 painter)))

and
square-limit
can be expressed as
²⁵

(define (square-limit painter n)
  (let ((combine4 (square-of-four flip-horiz identity
                                  rotate180 flip-vert)))
    (combine4 (corner-split painter n))))