Structure and Interpretation of Computer Programs (66 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

This is unsuitable for infinite streams, however,
because it takes all the elements from the first stream before
incorporating the second stream.
In particular, if we try to generate all pairs of positive integers using
(pairs integers integers)
our stream of results will first try to run through all pairs with the
first integer equal to 1, and hence will never produce pairs with any
other value of the first integer.
To handle infinite streams, we need to devise an order of combination
that ensures that every element will eventually be reached if we let
our program run long enough. An elegant way to accomplish this is
with the following
interleave
procedure:
68
(define (interleave s1 s2)
(if (stream-null? s1)
s2
(cons-stream (stream-car s1)
(interleave s2 (stream-cdr s1)))))
Since
interleave
takes elements alternately from the two streams,
every element of the second stream will eventually find its way into
the interleaved stream, even if the first stream is infinite.
We can thus generate the required stream of pairs as
(define (pairs s t)
(cons-stream
(list (stream-car s) (stream-car t))
(interleave
(stream-map (lambda (x) (list (stream-car s) x))
(stream-cdr t))
(pairs (stream-cdr s) (stream-cdr t)))))
Exercise 3.66.
Examine the stream
(pairs integers integers)
. Can you make any general
comments about the order in which the pairs are placed into the
stream? For example, about how many pairs precede the pair (1,100)?
the pair (99,100)? the pair (100,100)? (If you can make precise
mathematical statements here, all the better. But feel free to give
more qualitative answers if you find yourself getting bogged down.)
Exercise 3.67.
Modify the
pairs
procedure so that
(pairs integers
integers)
will produce the stream of
all
pairs of integers
(
i
,
j
) (without the condition
i
<
j
). Hint: You will need to
mix in an additional stream.
Exercise 3.68.
Louis Reasoner thinks that building a stream of pairs from three
parts is unnecessarily complicated. Instead of separating the
pair (
S
0
,
T
0
) from the rest of the pairs in the first row,
he proposes to work with the whole first row, as follows:
(define (pairs s t)
(interleave
(stream-map (lambda (x) (list (stream-car s) x))
t)
(pairs (stream-cdr s) (stream-cdr t))))
Does this work? Consider what happens if we evaluate
(pairs integers integers)
using Louis's definition of
pairs
.
Exercise 3.69.
Write a procedure
triples
that takes three infinite
streams,
S
,
T
, and
U
, and produces the stream of triples
(
S
i
,
T
j
,
U
k
) such that
i
<
j
<
k
.
Use
triples
to
generate the stream of all
Pythagorean triples of positive integers,
i.e., the triples (
i
,
j
,
k
) such that
i
<
j
and
i
2
+
j
2
=
k
2
.
Exercise 3.70.
It would be nice to be able to generate streams in which the pairs
appear in some useful order, rather than in the order that results
from an
ad hoc
interleaving process. We can use a technique
similar to the
merge
procedure of exercise
3.56
, if we
define a way to say that one pair of integers is “less than”
another. One way to do this is to define a “weighting function”
W
(
i
,
j
) and stipulate that (
i
1
,
j
1
) is less than (
i
2
,
j
2
) if
W
(
i
1
,
j
1
) <
W
(
i
2
,
j
2
). Write a procedure
merge-weighted
that is like
merge
, except that
merge-weighted
takes an
additional argument
weight
, which is a procedure that computes
the weight of a pair, and is used to determine the order in which
elements should appear in the resulting merged stream.
69
Using this,
generalize
pairs
to a procedure
weighted-pairs
that
takes two streams, together with a procedure that computes a weighting
function, and generates the stream of pairs, ordered according to
weight. Use your procedure to generate
a. the stream of all pairs of positive integers (
i
,
j
) with
i
<
j
ordered according to the sum
i
+
j
b. the stream of all pairs of positive integers (
i
,
j
) with
i
<
j
, where neither
i
nor
j
is divisible by 2, 3, or 5, and the
pairs are ordered according to the sum 2
i
+ 3
j
+ 5
i
j
.
Exercise 3.71.
Numbers that can be expressed as the sum of two cubes in more than one
way are sometimes called
Ramanujan numbers
, in honor of the
mathematician Srinivasa Ramanujan.
70
Ordered streams of pairs provide an elegant solution to the problem of
computing these numbers. To find a number that can be written as the
sum of two cubes in two different ways, we need only generate the
stream of pairs of integers (
i
,
j
) weighted according to the sum
i
3
+
j
3
(see exercise
3.70
),
then search the stream for two consecutive pairs with the same
weight. Write a procedure to generate the Ramanujan numbers. The first
such number is 1,729. What are the next five?
Exercise 3.72.
In a similar way to exercise
3.71
generate
a stream of
all numbers that can be written as the sum of two squares in three
different ways (showing how they can be so written).
We began our discussion of streams by describing them as computational
analogs of the “signals” in signal-processing systems. In fact, we
can use streams to model signal-processing systems in a very direct
way, representing the values of a signal at successive time intervals
as consecutive elements of a stream. For instance, we can implement
an
integrator
or
summer
that, for an input stream
x
= (
x
i
), an initial value
C
, and a small increment
d
t
,
accumulates the sum
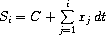
and returns the stream of values
S
= (
S
i
). The following
integral
procedure is reminiscent of the “implicit style” definition of the
stream of integers (section
3.5.2
):
(define (integral integrand initial-value dt)
(define int
(cons-stream initial-value
(add-streams (scale-stream integrand dt)
int)))
int)
 |
Figure
3.32
is a picture of a signal-processing system that
corresponds to the
integral
procedure. The input stream is
scaled by
d
t
and passed through an adder, whose output is passed
back through the same adder. The self-reference in the definition of
int
is reflected in the figure by the feedback loop that
connects the output of the adder to one of the inputs.
Exercise 3.73.
 v = v 0 + (1/ C )∫ 0 t i d t + R i
|
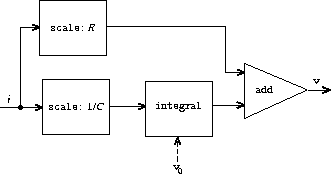
We can model electrical circuits using streams to represent the values
of currents or voltages at a sequence of times. For instance, suppose
we have an
RC circuit
consisting of a resistor of resistance
R
and a capacitor of capacitance
C
in series. The voltage response
v
of the circuit to an injected current
i
is determined by the
formula in figure
3.33
, whose structure is shown by the accompanying
signal-flow diagram.
Write a procedure
RC
that models this circuit.
RC
should
take as inputs the values of
R
,
C
, and
d
t
and should return a
procedure that takes as inputs a stream representing the current
i
and an initial value for the capacitor voltage
v
0
and produces as
output the stream of voltages
v
. For example, you should be able to
use
RC
to model an RC circuit with
R
= 5 ohms,
C
= 1 farad,
and a 0.5-second time step by evaluating
(define RC1 (RC 5 1
0.5))
. This defines
RC1
as a procedure that takes a stream
representing the time sequence of currents and an initial capacitor
voltage and produces the output stream of voltages.