Structure and Interpretation of Computer Programs (63 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

What is the value of
sum
after each of the above expressions is
evaluated? What is the printed response to evaluating the
stream-ref
and
display-stream
expressions? Would these responses
differ if we had implemented
(delay <
exp
>)
simply as
(lambda () <
exp
>)
without using the optimization provided by
memo-proc
? Explain.
We have seen how to support the illusion of manipulating streams
as complete entities even though, in actuality, we compute only
as much of the stream as we need to access. We can exploit this
technique to represent sequences efficiently as streams, even if the
sequences are very long. What is more striking, we can use streams to
represent sequences that are infinitely long. For instance, consider
the following definition of the stream of positive integers:
(define (integers-starting-from n)
(cons-stream n (integers-starting-from (+ n 1))))
(define integers (integers-starting-from 1))
This makes sense because
integers
will be a pair whose
car
is 1 and whose
cdr
is a promise to produce the integers
beginning with 2. This is an infinitely long stream, but in any given
time we can examine only a finite portion of it. Thus, our programs
will never know that the entire infinite stream is not there.
Using
integers
we can define other infinite streams, such as
the stream of integers that are not divisible by 7:
(define (divisible? x y) (= (remainder x y) 0))
(define no-sevens
(stream-filter (lambda (x) (not (divisible? x 7)))
integers))
Then we can find integers not divisible by 7 simply by accessing
elements of this stream:
(stream-ref no-sevens 100)
117
In analogy with
integers
, we can define the infinite stream of
Fibonacci numbers:
(define (fibgen a b)
(cons-stream a (fibgen b (+ a b))))
(define fibs (fibgen 0 1))
Fibs
is a pair whose
car
is 0 and whose
cdr
is a
promise to evaluate
(fibgen 1 1)
. When we evaluate this delayed
(fibgen 1 1)
, it
will produce a pair whose
car
is 1 and whose
cdr
is a
promise to evaluate
(fibgen 1 2)
, and so on.
For a look at a more exciting infinite stream, we can generalize the
no-sevens
example to construct the infinite stream of prime
numbers, using a method known as the
sieve of
Eratosthenes
.
60
We
start with the integers beginning with 2, which is the first prime.
To get the rest of the primes, we start by filtering the multiples of
2 from the rest of the integers. This leaves a stream beginning with
3, which is the next prime. Now we filter the multiples of 3 from the
rest of this stream. This leaves a stream beginning with 5, which is
the next prime, and so on. In other words, we construct the primes by
a sieving process, described as follows: To sieve a stream
S
,
form a stream whose first element is the first element of
S
and
the rest of which is obtained by filtering all multiples of the first element
of
S
out of the rest of
S
and sieving the result. This
process is readily described in terms of stream operations:
(define (sieve stream)
(cons-stream
(stream-car stream)
(sieve (stream-filter
(lambda (x)
(not (divisible? x (stream-car stream))))
(stream-cdr stream)))))
(define primes (sieve (integers-starting-from 2)))
Now to find a particular prime we need only ask for it:
(stream-ref primes 50)
233
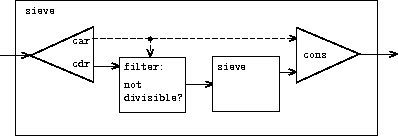
It is interesting to contemplate the signal-processing system set up
by
sieve
, shown in the
“Henderson diagram” in
figure
3.31
.
61
The input stream feeds into an
“un
cons
er” that separates the first element of the stream from the
rest of the stream.
The first element is used to construct a divisibility filter, through
which the rest is passed, and the output of the filter is fed to
another sieve box. Then the original first element is
cons
ed onto the
output of the internal sieve to form the output stream. Thus, not
only is the stream infinite, but the signal processor is also
infinite, because the sieve contains a sieve within it.
 |
The
integers
and
fibs
streams above were defined by
specifying “generating” procedures that explicitly compute the
stream elements one by one. An alternative way to specify streams is
to take advantage of delayed evaluation to define streams implicitly.
For example, the following expression defines the stream
ones
to
be an infinite stream of ones:
(define ones (cons-stream 1 ones))
This works much like the definition of a recursive procedure:
ones
is a pair whose
car
is 1 and whose
cdr
is a promise
to evaluate
ones
. Evaluating the
cdr
gives us again a 1
and a promise to evaluate
ones
, and so on.
We can do more interesting things by manipulating streams with
operations such as
add-streams
, which produces the elementwise
sum of two given streams:
62
(define (add-streams s1 s2)
(stream-map + s1 s2))
Now we can define the integers as follows:
(define integers (cons-stream 1 (add-streams ones integers)))
This defines
integers
to be a stream whose first element is 1
and the rest of which is the sum of
ones
and
integers
. Thus, the
second element of
integers
is 1 plus the first element of
integers
,
or 2; the third element of
integers
is 1 plus the second
element of
integers
, or 3; and so on. This definition works
because, at any point, enough of the
integers
stream has been
generated so that we can feed it back into the definition to produce
the next integer.
We can define the Fibonacci numbers in the same style:
(define fibs
(cons-stream 0
(cons-stream 1
(add-streams (stream-cdr fibs)
fibs))))
This definition says that
fibs
is a stream beginning with 0 and
1, such that the rest of the stream can be generated by adding
fibs
to itself shifted by one place:
| 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | ... = (stream-cdr fibs) | ||
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | ... = fibs | ||
| 0 | 1 | 1 | 2 | 3 | 5 | 8 | 13 | 21 | 34 | ... = fibs |
Scale-stream
is another useful procedure in formulating such stream definitions.
This multiplies each item in a stream by a given
constant:
(define (scale-stream stream factor)
(stream-map (lambda (x) (* x factor)) stream))
For example,
(define double (cons-stream 1 (scale-stream double 2)))
produces the stream of powers of 2: 1, 2, 4, 8, 16, 32,
...
.
An alternate definition of the stream of primes can be given by
starting with the integers and filtering them by testing for
primality. We will need the first prime, 2, to get started:
(define primes
(cons-stream
2
(stream-filter prime? (integers-starting-from 3))))
This definition is not so straightforward as it appears, because we
will test whether a number
n
is prime by checking whether
n
is
divisible by a prime (not by just any integer) less than or equal to
√
n
:
(define (prime? n)
(define (iter ps)
(cond ((> (square (stream-car ps)) n) true)
((divisible? n (stream-car ps)) false)
(else (iter (stream-cdr ps)))))
(iter primes))
This is a recursive definition, since
primes
is defined in terms
of the
prime?
predicate, which itself uses the
primes
stream. The reason this procedure works is that, at any point, enough
of the
primes
stream has been generated to test the primality of
the numbers we need to check next. That is, for every
n
we test for
primality, either
n
is not prime (in which case there is a prime
already generated that divides it) or
n
is prime (in which case
there is a prime already generated – i.e., a prime less than
n
– that is greater than √
n
).
63
Exercise 3.53.
Without running the program, describe the elements of the
stream defined by
(define s (cons-stream 1 (add-streams s s)))
Exercise 3.54.
Define a procedure
mul-streams
, analogous to
add-streams
,
that produces the elementwise product of its two input streams.
Use this together with the stream of
integers
to complete the
following definition of the stream whose
n
th element (counting from 0)
is
n
+ 1 factorial:
(define factorials (cons-stream 1 (mul-streams <
??
> <
??
>)))
Exercise 3.55.
Define a procedure
partial-sums
that takes as argument a
stream
S
and returns the stream whose
elements are
S
0
,
S
0
+
S
1
,
S
0
+
S
1
+
S
2
,
...
. For example,
(partial-sums integers)
should be the stream
1, 3, 6, 10, 15,
...
.
Exercise 3.56.
A famous problem, first raised by
R. Hamming, is to enumerate, in
ascending order with no repetitions, all positive integers with no
prime factors other than 2, 3, or 5. One obvious way to do this is to
simply test each integer in turn to see whether it has any factors
other than 2, 3, and 5. But this is very inefficient, since, as the
integers get larger, fewer and fewer of them fit the requirement. As
an alternative, let us call the required stream of numbers
S
and
notice the following facts about it.
- S
begins with 1. - The elements of
(scale-stream S 2)
are also
elements of
S
. - The same is true for
(scale-stream S 3)
and
(scale-stream 5 S)
. - These are all the elements of
S
.
Now all we have to do is combine elements from these sources.
For this we define a procedure
merge
that combines two ordered
streams into one ordered result stream, eliminating repetitions:
(define (merge s1 s2)
(cond ((stream-null? s1) s2)
((stream-null? s2) s1)
(else
(let ((s1car (stream-car s1))
(s2car (stream-car s2)))
(cond ((< s1car s2car)
(cons-stream s1car (merge (stream-cdr s1) s2)))
((> s1car s2car)
(cons-stream s2car (merge s1 (stream-cdr s2))))
(else
(cons-stream s1car
(merge (stream-cdr s1)
(stream-cdr s2)))))))))
Then the required stream may be constructed with
merge
, as
follows:
(define S (cons-stream 1 (merge <
??
> <
??
>)))
Fill in the missing expressions in the places marked <
??
> above.
Exercise 3.57.
How many additions are performed when we compute the
n
th Fibonacci
number using the definition of
fibs
based on the
add-streams
procedure? Show that the number of additions would be
exponentially greater if we had implemented
(delay <
exp
>)
simply as
(lambda () <
exp
>)
,
without using the optimization provided by the
memo-proc
procedure described in section
3.5.1
.
64