Structure and Interpretation of Computer Programs (48 page)

When we introduced compound procedures in chapter 1, we used the
substitution model of evaluation
(section 
1.1.5
) to define what is meant by
applying a procedure to arguments:

• To apply a compound procedure to arguments, evaluate the body of the
  procedure with each formal parameter replaced by the corresponding
  argument.
  

Once we admit assignment into our programming language, such a
definition is no longer adequate. In particular,
section 
3.1.3
argued that, in the presence of
assignment, a variable can no longer be considered to be merely a name
for a value. Rather, a variable must somehow designate a “place” in
which values can be stored. In our new model of evaluation, these
places will be maintained in structures called
environments
.

An environment is a sequence of
frames
. Each frame is a table
(possibly empty) of
bindings
, which associate variable names with
their corresponding values. (A single frame may contain at most one
binding for any variable.) Each frame also has a pointer to its
enclosing environment
, unless, for the purposes of discussion, the
frame is considered to be
global
. The
value of a variable
with respect to an environment is the value given by the binding of
the variable in the first frame in the environment that contains a
binding for that variable. If no frame in the sequence specifies a
binding for the variable, then the variable is said to be
unbound
in the environment.

Figure 3.1:
  A simple environment structure.

Figure 
3.1
shows a simple environment
structure consisting of three frames, labeled I, II, and III. In the
diagram, A, B, C, and D are pointers to environments. C and D point
to the same environment. The variables
z
and
x
are bound
in frame II, while
y
and
x
are bound in frame I. The
value of
x
in environment D is 3. The value of
x
with
respect to environment B is also 3. This is determined as follows: We
examine the first frame in the sequence (frame III) and do not find a
binding for
x
, so we proceed to the enclosing environment D and
find the binding in frame I. On the other hand, the value of
x
in environment A is 7, because the first frame in the sequence (frame
II) contains a binding of
x
to 7. With respect to environment
A, the binding of
x
to 7 in frame II is said to
shadow
the
binding of
x
to 3 in frame I.

The environment is crucial to the evaluation process,
because it determines the context in which an expression should be
evaluated. Indeed, one could say that expressions in a programming
language do not, in themselves, have any meaning. Rather, an
expression acquires a meaning only with respect to some environment in
which it is evaluated. Even the interpretation of an expression as
straightforward as
(+ 1 1)
depends on an understanding that one
is operating in a context in which
+
is the symbol for addition.
Thus, in our model of evaluation we will always speak of evaluating an
expression with respect to some environment. To describe interactions
with the interpreter, we will suppose that there is a
global
environment, consisting of a single frame (with no enclosing
environment) that includes values for the symbols associated with the
primitive procedures. For example, the idea that
+
is the
symbol for addition is captured by saying that the symbol
+
is
bound in the global environment to the primitive addition procedure.

The overall specification of how the interpreter evaluates a
combination remains the same as when we first introduced it in
section 
1.1.3
:

• To evaluate a combination:
  

1.  Evaluate the subexpressions of the
combination.
¹²

2.  Apply the value of the operator subexpression to the values of the
operand subexpressions.

The environment model of evaluation replaces the substitution model in
specifying what it means to apply a compound procedure to arguments.

In the environment model of evaluation, a procedure is always a pair
consisting of some code and a pointer to an environment. Procedures
are created in one way only: by evaluating a
lambda
expression.
This produces a procedure whose code is obtained from the text of the
lambda
expression and whose environment is the environment in
which the
lambda
expression was evaluated to produce the
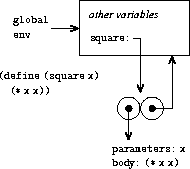
procedure. For example, consider the procedure definition

(define (square x)
  (* x x))

evaluated in the global environment. The procedure definition syntax
is just syntactic sugar for an underlying implicit
lambda
expression. It would have been equivalent to have used

(define square
  (lambda (x) (* x x)))

which evaluates
(lambda (x) (* x x))
and binds
square
to the resulting value, all in the global environment.

Figure 
3.2
shows the result of evaluating this
define
expression. The procedure object is a pair whose code
specifies that the procedure has one formal parameter, namely
x
,
and a procedure body
(* x x)
. The environment part of the
procedure is a pointer to the global environment, since that is the
environment in which the
lambda
expression was evaluated to
produce the procedure. A new binding, which associates the procedure
object with the symbol
square
, has been added to the global
frame. In general,
define
creates definitions by adding
bindings to frames.

Figure 3.2:
  Environment structure produced by
evaluating
(define (square x) (* x x))
in the global environment.

Now that we have seen how procedures are created, we can describe how
procedures are applied. The environment model specifies: To apply a
procedure to arguments, create a new environment containing a frame
that binds the parameters to the values of the arguments. The
enclosing environment of this frame is the environment specified by
the procedure. Now, within this new environment, evaluate the
procedure body.

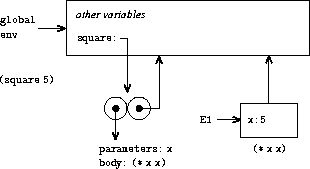
To show how this rule is followed, figure 
3.3
illustrates the environment structure created by evaluating the
expression
(square 5)
in the global environment, where
square
is the procedure generated in
figure 
3.2
. Applying the procedure results in
the creation of a new environment, labeled E1 in the figure, that
begins with a frame in which
x
, the formal parameter for the
procedure, is bound to the argument 5. The pointer leading upward
from this frame shows that the frame's enclosing environment is the
global environment. The global environment is chosen here, because
this is the environment that is indicated as part of the
square
procedure object. Within E1, we evaluate the body of the procedure,
(* x x)
. Since the value of
x
in E1 is 5, the result is
(* 5 5)
, or 25.

Figure 3.3:
  Environment created by evaluating
(square 5)
in the global environment.

The environment model of procedure application can be summarized by
two rules:

• A procedure object is applied to a set of arguments by
  constructing a frame, binding the formal parameters of the procedure
  to the arguments of the call, and then evaluating the body of
  the procedure in the context of the new environment constructed. The
  new frame has as its enclosing environment the environment part of the
  procedure object being applied.
  
• A procedure is created by evaluating a
  lambda
  expression relative to a given environment. The resulting procedure
  object is a pair consisting of the text of the
  lambda
  expression
  and a pointer to the environment in which the procedure was created.
  

We also specify that defining a symbol using
define
creates a
binding in the current environment frame and assigns to the symbol the
indicated value.
¹³
Finally, we specify the behavior of
set!
, the operation that forced us to introduce the environment
model in the first place. Evaluating the expression
(set!
<
variable
> <
value
>)
in some environment locates the binding of
the variable in the environment and changes that binding to indicate
the new value. That is, one finds the first frame in the environment
that contains a binding for the variable and modifies that frame. If
the variable is unbound in the environment, then
set!
signals
an error.

These evaluation rules, though considerably more complex than the
substitution model, are still reasonably straightforward. Moreover,
the evaluation model, though abstract, provides a correct description
of how the interpreter evaluates expressions. In chapter 4 we shall
see how this model can serve as a blueprint for implementing a working
interpreter. The following sections elaborate the details of the
model by analyzing some illustrative programs.

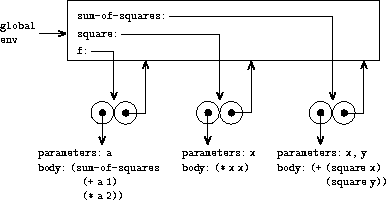
When we introduced the substitution model in
section 
1.1.5
we showed how the combination
(f 5)
evaluates to 136, given the following procedure
definitions:

(define (square x)
  (* x x))
(define (sum-of-squares x y)
  (+ (square x) (square y)))
(define (f a)
  (sum-of-squares (+ a 1) (* a 2)))

We can analyze the same example using the environment model.
Figure 
3.4
shows the three procedure objects
created by evaluating the definitions of
f
,
square
, and
sum-of-squares
in the global environment. Each procedure object
consists of some code, together with a pointer to the global
environment.

Figure 3.4:
  Procedure objects in the global frame.