Structure and Interpretation of Computer Programs (44 page)
Read Structure and Interpretation of Computer Programs Online
Authors: Harold Abelson and Gerald Jay Sussman with Julie Sussman

(define p1 (make-polynomial 'x '((1 1)(0 1))))
(define p2 (make-polynomial 'x '((3 1)(0 -1))))
(define p3 (make-polynomial 'x '((1 1))))
(define p4 (make-polynomial 'x '((2 1)(0 -1))))
(define rf1 (make-rational p1 p2))
(define rf2 (make-rational p3 p4))
(add rf1 rf2)
See if you get the correct answer, correctly reduced to lowest terms.
The GCD computation is at the heart of any system that does operations
on rational functions. The algorithm used above, although
mathematically straightforward, is extremely slow. The slowness is
due partly to the large number of division operations and partly to
the enormous size of the intermediate coefficients generated by the
pseudodivisions. One of the active areas in the development of
algebraic-manipulation systems is the design of better algorithms for
computing polynomial GCDs.
62
49
We also have to supply an almost identical
procedure to handle the types
(scheme-number complex)
.
50
See
exercise
2.82
for generalizations.
51
If we are
clever, we can usually get by with fewer than
n
2
coercion
procedures. For instance, if we know how to convert from type 1 to
type 2 and from type 2 to type 3, then we can use this knowledge to
convert from type 1 to type 3. This can greatly decrease the number
of coercion procedures we need to supply explicitly when we add a new
type to the system. If we are willing to build the required amount of
sophistication into our system, we can have it search the “graph” of
relations among types and automatically generate those coercion
procedures that can be inferred from the ones that are supplied
explicitly.
52
This statement, which also appears in the first edition of this book,
is just as true now as it was when we wrote it twelve years ago.
Developing a useful, general framework for expressing the relations
among different types of entities (what philosophers call
“ontology”) seems intractably difficult. The main difference
between the confusion that existed ten years ago and the confusion
that exists now is that now a variety of inadequate ontological
theories have been embodied in a plethora of correspondingly
inadequate programming languages. For example, much of the complexity
of
object-oriented programming languages – and the subtle and
confusing differences among contemporary object-oriented
languages – centers on the treatment of generic operations on
interrelated types. Our own discussion of computational objects in
chapter 3 avoids these issues entirely. Readers familiar with
object-oriented programming will notice that we have much to say in
chapter 3 about local state, but we do not even mention “classes” or
“inheritance.” In fact, we suspect that these problems cannot be
adequately addressed in terms of computer-language design alone,
without also drawing on work in knowledge representation and automated
reasoning.
53
A real number can be projected to an integer
using the
round
primitive, which returns the closest integer
to its argument.
54
On the other hand, we will allow
polynomials whose coefficients are themselves polynomials in other
variables. This will give us essentially the same representational
power as a full multivariate system, although it does lead to coercion
problems, as discussed below.
55
For univariate polynomials, giving
the value of a polynomial at a given set of points can be a
particularly good representation. This makes polynomial arithmetic
extremely simple. To obtain, for example, the sum of two polynomials
represented in this way, we need only add the values of the
polynomials at corresponding points. To transform back to a more
familiar representation, we can use the
Lagrange interpolation
formula, which shows how to recover the coefficients of a polynomial
of degree
n
given the values of the polynomial at
n
+ 1 points.
56
This operation is very much like the ordered
union-set
operation we developed in exercise
2.62
.
In fact, if we think of the terms of the polynomial as a set ordered
according to the power of the indeterminate, then the program that
produces the term list for a sum is almost identical to
union-set
.
57
To make
this work completely smoothly, we should also add to our generic
arithmetic system the ability to coerce a “number” to a polynomial
by regarding it as a polynomial of degree zero whose coefficient is
the number. This is necessary if we are going to perform operations
such as
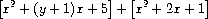
which requires adding the coefficient
y
+ 1 to the coefficient 2.
58
In these polynomial examples,
we assume that we have implemented the generic arithmetic system using
the type mechanism suggested in exercise
2.78
.
Thus, coefficients that are ordinary numbers will be represented as
the numbers themselves rather than as pairs whose
car
is the
symbol
scheme-number
.
59
Although
we are assuming that term
lists are ordered, we have implemented
adjoin-term
to simply
cons
the new term onto the existing term list. We can get away
with this so long as we guarantee that the procedures (such as
add-terms
) that use
adjoin-term
always call it with a higher-order
term than appears in the list. If we did not want to make such a
guarantee, we could have implemented
adjoin-term
to be similar
to the
adjoin-set
constructor for the ordered-list
representation of sets (exercise
2.61
).
60
The fact
that
Euclid's Algorithm works for polynomials is formalized in algebra
by saying that polynomials form a kind of algebraic domain called a
Euclidean ring
. A Euclidean ring is a domain that admits
addition, subtraction, and commutative multiplication, together with a
way of assigning to each element
x
of the ring a positive integer
“measure”
m
(
x
) with the properties that
m
(
x
y
)
>
m
(
x
) for
any nonzero
x
and
y
and that, given any
x
and
y
, there exists
a
q
such that
y
=
q
x
+
r
and either
r
= 0 or
m
(
r
)<
m
(
x
). From an
abstract point of view, this is what is needed to prove that Euclid's
Algorithm works. For the domain of integers, the measure
m
of an
integer is the absolute value of the integer itself. For the domain
of polynomials, the measure of a polynomial is its degree.
61
In an implementation like MIT Scheme, this produces a polynomial
that is indeed a divisor of
Q
1
and
Q
2
, but with rational coefficients.
In many other Scheme systems, in which division of integers can produce
limited-precision decimal numbers, we may fail to get a valid divisor.
62
One extremely efficient and
elegant method for computing
polynomial GCDs was discovered by
Richard
Zippel (1979). The method is a probabilistic algorithm, as is the
fast test for primality that we discussed in chapter 1. Zippel's book
(1993) describes this method, together with other ways to compute
polynomial GCDs.
Modularity, Objects, and State
M (Even while it changes, it stands still.) Heraclitus Plus ça change, plus c'est la même chose. Alphonse Karr |
The preceding chapters introduced the basic elements from which
programs are made. We saw how primitive procedures and primitive data
are combined to construct compound entities, and we learned that
abstraction is vital in helping us to cope with the complexity of
large systems. But these tools are not sufficient for designing
programs. Effective program synthesis also requires organizational
principles that can guide us in formulating the overall design of a
program. In particular, we need strategies to help us structure large
systems so that they will be
modular
, that is, so that they can
be divided “naturally” into coherent parts that can be separately
developed and maintained.
One powerful design strategy, which is particularly appropriate to the
construction of programs for modeling physical systems, is to base the
structure of our programs on the structure of the system being
modeled. For each object in the system, we construct a corresponding
computational object. For each system action, we define a symbolic
operation in our computational model. Our hope in using this strategy
is that extending the model to accommodate new objects or new actions
will require no strategic changes to the program, only the addition of
the new symbolic analogs of those objects or actions. If we have been
successful in our system organization, then to add a new feature or
debug an old one we will have to work on only a localized part of the
system.
To a large extent, then, the way we organize a large program is
dictated by our perception of the system to be modeled. In this
chapter we will investigate two prominent organizational strategies
arising from two rather different “world views” of the structure of
systems. The first organizational strategy concentrates on
objects
, viewing a large system as a collection of distinct objects
whose behaviors may change over time. An alternative organizational
strategy concentrates on the
streams
of information that flow in
the system, much as an electrical engineer views a signal-processing
system.
Both the object-based approach and the stream-processing approach
raise significant linguistic issues in programming.
With objects, we must be concerned with how a computational object can
change and yet maintain its identity. This will force us to abandon
our old substitution model of computation
(section
1.1.5
) in favor of a more mechanistic
but less theoretically tractable
environment model
of
computation. The difficulties of dealing with objects, change, and
identity are a fundamental consequence of the need to grapple with
time in our computational models. These difficulties become even
greater when we allow the possibility of concurrent execution of
programs. The stream approach can be most fully exploited when we
decouple simulated time in our model from the order of the events that
take place in the computer during evaluation. We will accomplish this
using a technique known as
delayed evaluation
.
We ordinarily view the world as populated by independent objects, each
of which has a state that changes over time. An object is said to
“have state” if its behavior is influenced by its history. A bank
account, for example, has state in that the answer to the question
“Can I withdraw $100?” depends upon the history of deposit and
withdrawal transactions. We can characterize an object's state by one
or more
state variables
, which among them maintain enough
information about history to determine the object's current behavior.
In a simple banking system, we could characterize the state of an
account by a current balance rather than by remembering the entire
history of account transactions.
