Structure and Interpretation of Computer Programs (39 page)

(define (install-rational-package)
  
;; internal procedures
  (define (numer x) (car x))
  (define (denom x) (cdr x))
  (define (make-rat n d)
    (let ((g (gcd n d)))
      (cons (/ n g) (/ d g))))
  (define (add-rat x y)
    (make-rat (+ (* (numer x) (denom y))
                 (* (numer y) (denom x)))
              (* (denom x) (denom y))))
  (define (sub-rat x y)
    (make-rat (- (* (numer x) (denom y))
                 (* (numer y) (denom x)))
              (* (denom x) (denom y))))
  (define (mul-rat x y)
    (make-rat (* (numer x) (numer y))
              (* (denom x) (denom y))))
  (define (div-rat x y)
    (make-rat (* (numer x) (denom y))
              (* (denom x) (numer y))))
  
;; interface to rest of the system
  (define (tag x) (attach-tag 'rational x))
  (put 'add '(rational rational)
       (lambda (x y) (tag (add-rat x y))))
  (put 'sub '(rational rational)
       (lambda (x y) (tag (sub-rat x y))))
  (put 'mul '(rational rational)
       (lambda (x y) (tag (mul-rat x y))))
  (put 'div '(rational rational)
       (lambda (x y) (tag (div-rat x y))))
  (put 'make 'rational
       (lambda (n d) (tag (make-rat n d))))
  'done)
(define (make-rational n d)
  ((get 'make 'rational) n d))

We can install a similar package to handle complex numbers, using the
tag
complex
. In creating the package, we extract from the table
the operations
make-from-real-imag
and
make-from-mag-ang
that were defined by the rectangular and polar packages.
Additivity
permits us to use, as the internal operations, the same
add-complex
,
sub-complex
,
mul-complex
, and
div-complex
procedures from
section 
2.4.1
.

(define (install-complex-package)
  
;; imported procedures from rectangular and polar packages
  (define (make-from-real-imag x y)
    ((get 'make-from-real-imag 'rectangular) x y))
  (define (make-from-mag-ang r a)
    ((get 'make-from-mag-ang 'polar) r a))
  
;; internal procedures
  (define (add-complex z1 z2)
    (make-from-real-imag (+ (real-part z1) (real-part z2))
                         (+ (imag-part z1) (imag-part z2))))
  (define (sub-complex z1 z2)
    (make-from-real-imag (- (real-part z1) (real-part z2))
                         (- (imag-part z1) (imag-part z2))))
  (define (mul-complex z1 z2)
    (make-from-mag-ang (* (magnitude z1) (magnitude z2))
                       (+ (angle z1) (angle z2))))
  (define (div-complex z1 z2)
    (make-from-mag-ang (/ (magnitude z1) (magnitude z2))
                       (- (angle z1) (angle z2))))
  
;; interface to rest of the system
  (define (tag z) (attach-tag 'complex z))
  (put 'add '(complex complex)
       (lambda (z1 z2) (tag (add-complex z1 z2))))
  (put 'sub '(complex complex)
       (lambda (z1 z2) (tag (sub-complex z1 z2))))
  (put 'mul '(complex complex)
       (lambda (z1 z2) (tag (mul-complex z1 z2))))
  (put 'div '(complex complex)
       (lambda (z1 z2) (tag (div-complex z1 z2))))
  (put 'make-from-real-imag 'complex
       (lambda (x y) (tag (make-from-real-imag x y))))
  (put 'make-from-mag-ang 'complex
       (lambda (r a) (tag (make-from-mag-ang r a))))
  'done)

Programs outside the complex-number package can construct complex
numbers either from real and imaginary parts or from magnitudes and
angles. Notice how the underlying procedures, originally defined in
the rectangular and polar packages, are exported to the complex
package, and exported from there to the outside world.

(define (make-complex-from-real-imag x y)
  ((get 'make-from-real-imag 'complex) x y))
(define (make-complex-from-mag-ang r a)
  ((get 'make-from-mag-ang 'complex) r a))

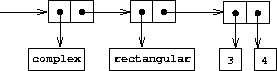
What we have here is a two-level tag system. A typical complex number,
such as 3 + 4
i
in rectangular form, would be
represented as shown in figure 
2.24
.
The outer tag (
complex
) is used to direct the number to the
complex package. Once within the complex package, the next tag (
rectangular
) is used to direct the number to the rectangular package.
In a large and complicated system there might be many levels, each
interfaced with the next by means of generic operations. As a data
object is passed “downward,” the outer tag that is used to direct
it to the appropriate package is stripped off (by applying
contents
) and the next level of tag (if any) becomes visible to be used for
further dispatching.

Figure 2.24:
  Representation of 3 + 4
i
in rectangular form.

In the above packages, we used
add-rat
,
add-complex
, and
the other arithmetic procedures exactly as originally written.
Once these definitions are internal to different installation procedures,
however, they no longer need names that are distinct from each other:
we could simply name them
add
,
sub
,
mul
, and
div
in both packages.

Exercise 2.77.
  Louis Reasoner tries to evaluate the
expression
(magnitude z)
where
z
is the object
shown in figure 
2.24
. To his
surprise, instead of the answer 5
he gets an error message from
apply-generic
,
saying there is no method for the operation
magnitude
on the types
(complex)
.
He shows this interaction to Alyssa P. Hacker, who says
“The problem is that the complex-number selectors were never
defined for
complex
numbers, just for
polar
and
rectangular
numbers. All you have to do to make this work is add the following
to the
complex
package:”

(put 'real-part '(complex) real-part)
(put 'imag-part '(complex) imag-part)
(put 'magnitude '(complex) magnitude)
(put 'angle '(complex) angle)

Describe in detail why this works. As an example, trace through all
the procedures called in evaluating the expression
(magnitude z)
where
z
is the object shown in
figure 
2.24
. In particular, how many
times is
apply-generic
invoked? What procedure is dispatched to
in each case?

Exercise 2.78.
  
The internal procedures in the
scheme-number
package are essentially
nothing more than calls to the primitive procedures
+
,
-
,
etc. It was not possible to use the primitives of the language
directly because our type-tag system requires that each data
object have a type attached to it. In fact, however, all Lisp
implementations do have a type system, which they use internally.
Primitive predicates such as
symbol?
and
number?
determine whether data objects have particular types. Modify the
definitions of
type-tag
,
contents
, and
attach-tag
from section 
2.4.2
so that our generic system takes
advantage of Scheme's internal type system. That is to say, the system
should work as before except that ordinary numbers should be
represented simply as Scheme numbers rather than as pairs whose
car
is
the symbol
scheme-number
.

Exercise 2.79.
  
Define a generic equality predicate
equ?
that tests the equality
of two numbers, and install it in the generic arithmetic
package. This operation should work for ordinary numbers, rational numbers, and
complex numbers.

Exercise 2.80.
  
Define a generic
predicate
=zero?
that tests if its argument is zero,
and install it in the generic arithmetic package. This
operation should work for ordinary numbers, rational numbers, and
complex numbers.

We have seen how to define a unified arithmetic system that
encompasses ordinary numbers, complex numbers, rational numbers, and
any other type of number we might decide to invent, but we have
ignored an important issue. The operations we have defined so far
treat the different data types as being completely independent. Thus,
there are separate packages for adding, say, two ordinary numbers, or
two complex numbers. What we have not yet considered is the fact that
it is meaningful to define operations that cross the type boundaries,
such as the addition of a complex number to an ordinary number. We
have gone to great pains to introduce barriers between parts of our
programs so that they can be developed and understood separately. We
would like to introduce the cross-type operations in some carefully
controlled way, so that we can support them
without seriously violating our module boundaries.

One way to handle cross-type operations is to design a different
procedure for each possible combination of types for which the
operation is valid. For example, we could extend the complex-number
package so that it provides a procedure for adding complex numbers to
ordinary numbers and installs this in the table using the tag
(complex scheme-number)
:
⁴⁹

;; to be included in the complex package
(define (add-complex-to-schemenum z x)
  (make-from-real-imag (+ (real-part z) x)
                       (imag-part z)))
(put 'add '(complex scheme-number)
     (lambda (z x) (tag (add-complex-to-schemenum z x))))

This technique works, but it is cumbersome. With such a system, the
cost of introducing a new type is not just the construction of the
package of procedures for that type but also the construction and
installation of the procedures that implement the cross-type
operations. This can easily be much more code than is needed to
define the operations on the type itself. The method also undermines
our ability to combine separate packages additively, or
least to limit the extent to which the implementors of the individual
packages need to take account of other packages. For instance, in the
example above, it seems reasonable that handling mixed operations on
complex numbers and ordinary numbers should be the responsibility of
the complex-number package. Combining rational numbers and complex
numbers, however, might be done by the complex package, by the
rational package, or by some third package that uses operations
extracted from these two packages. Formulating coherent policies on the
division of responsibility among packages can be an overwhelming task
in designing systems with many packages and many cross-type
operations.

In the general situation of completely unrelated operations acting on
completely unrelated types, implementing explicit cross-type
operations, cumbersome though it may be, is the best that one can hope
for. Fortunately, we can usually do better by taking advantage of
additional structure that may be latent in our type system. Often the
different data types are not completely independent, and there may be
ways by which objects of one type may be viewed as being of another
type. This process is called
coercion
. For example, if we are
asked to arithmetically combine an ordinary number with a complex
number, we can view the ordinary number as a complex number whose
imaginary part is zero. This transforms the problem to that of
combining two complex numbers, which can be handled in the ordinary
way by the complex-arithmetic package.

In general, we can implement this idea by designing coercion
procedures that transform an object of one type into an equivalent
object of another type. Here is a typical coercion procedure, which
transforms a given ordinary number to a complex number with that real
part and zero imaginary part:

(define (scheme-number->complex n)
  (make-complex-from-real-imag (contents n) 0))

We install these coercion procedures in a special coercion table,
indexed under the names of the two types:

(put-coercion 'scheme-number 'complex scheme-number->complex)

(We assume that there are
put-coercion
and
get-coercion
procedures available for manipulating this table.) Generally some of
the slots in the table will be empty, because it is not generally
possible to coerce an arbitrary data object of each type into all
other types. For example, there is no way to coerce an arbitrary
complex number to an ordinary number, so there will be no general
complex->scheme-number
procedure included in the table.

Once the coercion table has been set up, we can handle coercion in a
uniform manner by modifying the
apply-generic
procedure of
section 
2.4.3
. When asked to apply an operation, we
first check whether the operation is defined for the arguments' types,
just as before. If so, we dispatch to the procedure found in the
operation-and-type table.
Otherwise, we try coercion. For simplicity, we consider only the case
where there are two arguments.
⁵⁰
We
check the coercion table to see if objects of the first type can
be coerced to the second type. If so, we coerce the first argument and try the
operation again. If objects of the first type cannot in general be coerced to
the second type, we try the coercion the other way around to see if there is a
way to coerce the second argument to the type of the first argument.
Finally, if there
is no known way to coerce either type to the other type, we give up.
Here is the procedure: