Structure and Interpretation of Computer Programs (40 page)

(define (apply-generic op . args)
  (let ((type-tags (map type-tag args)))
    (let ((proc (get op type-tags)))
      (if proc
          (apply proc (map contents args))
          (if (= (length args) 2)
              (let ((type1 (car type-tags))
                    (type2 (cadr type-tags))
                    (a1 (car args))
                    (a2 (cadr args)))
                (let ((t1->t2 (get-coercion type1 type2))
                      (t2->t1 (get-coercion type2 type1)))
                  (cond (t1->t2
                         (apply-generic op (t1->t2 a1) a2))
                        (t2->t1
                         (apply-generic op a1 (t2->t1 a2)))
                        (else
                         (error "No method for these types"
                                (list op type-tags))))))
              (error "No method for these types"
                     (list op type-tags)))))))

This coercion scheme has many advantages over the method of defining
explicit cross-type operations, as outlined above. Although we still
need to write coercion procedures to relate the types (possibly
n
²
procedures for a system with
n
types), we need to write only one
procedure for each pair of types rather than a different procedure for
each collection of types and each generic operation.
⁵¹
What we are counting on here is the fact that the
appropriate transformation between types depends only on the types
themselves, not on the operation to be applied.

On the other hand, there may be applications for which our coercion
scheme is not general enough. Even when neither of the objects to be
combined can be converted to the type of the other it may still be
possible to perform the operation by converting both objects to a
third type. In order to deal with such complexity and still preserve
modularity in our programs, it is usually necessary to build systems
that take advantage of still further structure in the relations among
types, as we discuss next.

The coercion scheme presented above relied on the existence of natural
relations between pairs of types. Often there is more “global”
structure in how the different types relate to each other. For
instance, suppose we are building a generic arithmetic system to
handle integers, rational numbers, real numbers, and complex numbers.
In such a system, it is quite natural to regard an integer as a
special kind of rational number, which is in turn a special kind of
real number, which is in turn a special kind of complex number. What
we actually have is a so-called
hierarchy of types
, in which,
for example, integers are a
subtype
of rational numbers (i.e.,
any operation that can be applied to a rational number can
automatically be applied to an integer). Conversely, we say that
rational numbers form a
supertype
of integers. The particular
hierarchy we have here is of a very simple kind, in which each type
has at most one supertype and at most one subtype. Such a structure,
called a
tower
, is illustrated in figure 
2.25
.

Figure 2.25:
  A tower of types.

If we have a tower structure, then we can greatly simplify the problem
of adding a new type to the hierarchy, for we need only specify how
the new type is embedded in the next supertype above it and how it is
the supertype of the type below it. For example, if we want to add an
integer to a complex number, we need not explicitly define a special
coercion procedure
integer->complex
. Instead, we define how an
integer can be transformed into a rational number, how a rational
number is transformed into a real number, and how a real number is
transformed into a complex number. We then allow the system to
transform the integer into a complex number through these steps and
then add the two complex numbers.

We can redesign our
apply-generic
procedure in the following
way: For each type, we need to supply a
raise
procedure, which
“raises” objects of that type one level in the tower. Then when the
system is required to operate on objects of different types it can
successively raise the lower types until all the objects are at
the same level in the tower. (Exercises 
2.83
and  
2.84
concern the details of implementing such a strategy.)

Another advantage of a tower is that we can easily implement the
notion that every type “inherits” all operations defined on a
supertype. For instance, if we do not supply a special procedure for
finding the real part of an integer, we should nevertheless expect
that
real-part
will be defined for integers by virtue of the
fact that integers are a subtype of complex numbers. In a tower, we
can arrange for this to happen in a uniform way by modifying
apply-generic
. If the required operation is not directly defined for
the type of the object given, we raise the object to its supertype and
try again. We thus crawl up the tower, transforming our argument as we
go, until we either find a level at which the desired operation can be
performed or hit the top (in which case we give up).

Yet another advantage of a tower over a more general hierarchy is that
it gives us a simple way to “lower” a data object to the simplest
representation. For example, if we add 2 + 3
i
to 4 - 3
i
, it would be
nice to obtain the answer as the integer 6 rather than as the complex
number 6 + 0
i
. Exercise 
2.85
discusses a way to implement
such a lowering operation. (The trick is that we need a general way
to distinguish those objects that can be lowered, such as 6 + 0
i
, from
those that cannot, such as 6 + 2
i
.)

Figure 2.26:
  Relations among types of geometric figures.

If the data types in our system can be naturally arranged in a tower,
this greatly simplifies the problems of dealing with generic operations
on different types, as we have seen. Unfortunately, this is usually
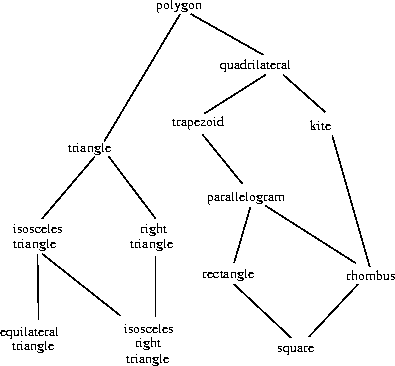
not the case. Figure 
2.26
illustrates a
more complex arrangement of mixed types, this one showing relations
among different types of geometric figures. We see that, in general,
a type may have more than one subtype. Triangles and quadrilaterals,
for instance, are both subtypes of polygons. In addition, a type may
have more than one supertype. For example, an isosceles right
triangle may be regarded either as an isosceles triangle or as a right
triangle. This multiple-supertypes issue is particularly thorny,
since it means that there is no unique way to “raise” a type in the
hierarchy. Finding the “correct” supertype in which to apply an
operation to an object may involve considerable searching through the
entire type network on the part of a procedure such as
apply-generic
. Since there generally are multiple subtypes for a
type, there is a similar problem in coercing a value “down” the type
hierarchy. Dealing with large numbers of interrelated types while
still preserving modularity in the design of large systems is very
difficult, and is an area of much current research.
⁵²

Exercise 2.81.
  
Louis Reasoner has noticed that
apply-generic
may try to
coerce the arguments to each other's type even if they already have
the same type. Therefore, he reasons, we need to put procedures
in the coercion table to "coerce" arguments of each type to their
own type. For example, in addition to the
scheme-number->complex
coercion shown above, he would do:

(define (scheme-number->scheme-number n) n)
(define (complex->complex z) z)
(put-coercion 'scheme-number 'scheme-number
              scheme-number->scheme-number)
(put-coercion 'complex 'complex complex->complex)

a. With Louis's coercion procedures installed, what happens if
apply-generic
is called with two arguments of type
scheme-number
or two arguments of
type
complex
for an operation that is not found in the table for those
types? For example, assume that we've defined a generic exponentiation
operation:

(define (exp x y) (apply-generic 'exp x y))

and have put a procedure for exponentiation in the Scheme-number
package but not in any other package:

;; following added to Scheme-number package
(put 'exp '(scheme-number scheme-number)
     (lambda (x y) (tag (expt x y)))) 
; using primitive 
expt

What happens if we call
exp
with two complex numbers as arguments?

b. Is Louis correct that something had to be done about
coercion with arguments of the same type, or does
apply-generic
work correctly as is?

c. Modify
apply-generic
so that it doesn't try coercion if
the two arguments have the same type.

Exercise 2.82.
  
Show how to generalize
apply-generic
to handle
coercion in the general case of multiple arguments. One strategy is
to attempt to coerce all the arguments to the type of the first argument, then
to the type of the second argument, and so on. Give an example of a situation
where this strategy (and likewise the two-argument version given
above) is not sufficiently general. (Hint: Consider the case where
there are some suitable mixed-type operations present in the table
that will not be tried.)

Exercise 2.83.
  
Suppose you are designing a generic arithmetic system for dealing with
the tower of types shown in figure 
2.25
:
integer, rational, real, complex. For
each type (except complex), design a procedure that raises objects of
that type one level in the tower. Show how to install a generic
raise
operation that will work for each type (except complex).

Exercise 2.84.
  
Using the
raise
operation of exercise 
2.83
, modify the
apply-generic
procedure so that it coerces its arguments to have the
same type by the method of successive raising, as discussed in this
section. You will need to devise a way to test which of two types is
higher in the tower. Do this in a manner that is “compatible” with
the rest of the system and will not lead to problems in adding new
levels to the tower.

Exercise 2.85.
  
This section mentioned a method for “simplifying” a data object
by lowering it in the tower of types as far as possible. Design
a procedure
drop
that accomplishes this for the tower described
in exercise 
2.83
. The key is to decide, in some general way, whether
an object can be lowered. For example, the complex number 1.5 + 0
i
can be lowered as far as
real
, the complex number 1 + 0
i
can be
lowered as far as
integer
, and the complex number 2 + 3
i
cannot
be lowered at all. Here is a plan for determining whether an object
can be lowered: Begin by defining a generic operation
project
that “pushes” an object down in the tower. For example, projecting
a complex number would involve throwing away the imaginary part. Then
a number can be dropped if, when we
project
it and
raise
the result back to the type we started with, we end up with something
equal to what we started with. Show how to implement this idea in
detail, by writing a
drop
procedure that drops an object as far
as possible. You will need to design the various projection
operations
⁵³
and install
project
as a generic operation in
the system. You will also need to make use of a generic equality
predicate, such as described in exercise 
2.79
. Finally, use
drop
to rewrite
apply-generic
from exercise 
2.84
so that it
“simplifies” its answers.