Structure and Interpretation of Computer Programs (38 page)

d.  In this simple algebraic manipulator the type of an expression is
the algebraic operator that binds it together. Suppose, however, we
indexed the procedures in the opposite way, so that the dispatch line
in
deriv
looked like

((get (operator exp) 'deriv) (operands exp) var)

What corresponding changes to the derivative system are required?

Exercise 2.74.
  
Insatiable Enterprises, Inc., is a highly decentralized conglomerate
company consisting of a large number of independent divisions located
all over the world. The company's computer facilities have just been
interconnected by means of a clever network-interfacing scheme that
makes the entire network appear to any user to be a single computer.
Insatiable's president, in her first attempt to exploit the ability of
the network to extract administrative information from division files,
is dismayed to discover that, although all the division files have
been implemented as data structures in Scheme, the particular data
structure used varies from division to division. A meeting of
division managers is hastily called to search for a strategy to
integrate the files that will satisfy headquarters' needs while
preserving the existing autonomy of the divisions.

Show how such a strategy can be implemented with data-directed
programming. As an example, suppose that each division's personnel
records consist of a single file, which contains a set of records
keyed on employees' names. The structure of the set varies from
division to division. Furthermore, each employee's record is itself a
set (structured differently from division to division) that contains
information keyed under identifiers such as
address
and
salary
. In particular:

a.  Implement for headquarters a
get-record
procedure that
retrieves a specified employee's record from a specified personnel
file. The procedure should be applicable to any division's file.
Explain how the individual divisions' files should be structured. In
particular, what type information must be supplied?

b.  Implement for headquarters a
get-salary
procedure that
returns the salary information from a given employee's record from any
division's personnel file. How should the record be structured in
order to make this operation work?

c.  Implement for headquarters a
find-employee-record
procedure.
This should search all the divisions' files for the record of a given
employee and return the record. Assume that this procedure takes as
arguments an employee's name and a list of all the divisions' files.

d.  When Insatiable takes over a new company, what changes must
be made in order to incorporate the new personnel information into the
central system?

The key idea of data-directed programming is to handle generic
operations in programs by dealing explicitly with operation-and-type
tables, such as the table in figure 
2.22
. The
style of programming we used in section 
2.4.2
organized the required dispatching on type by having each operation
take care of its own dispatching. In effect, this decomposes the
operation-and-type table into rows, with each generic operation
procedure representing a row of the table.

An alternative implementation strategy is to decompose the table into
columns and, instead of using “intelligent operations” that dispatch
on data types, to work with “intelligent data objects” that dispatch
on operation names. We can do this by arranging things so that a data
object, such as a rectangular number, is represented as a procedure
that takes as input the required operation name and performs the
operation indicated. In such a discipline,
make-from-real-imag
could be written as

(define (make-from-real-imag x y)
  (define (dispatch op)
    (cond ((eq? op 'real-part) x)
          ((eq? op 'imag-part) y)
          ((eq? op 'magnitude)
           (sqrt (+ (square x) (square y))))
          ((eq? op 'angle) (atan y x))
          (else
           (error "Unknown op -- MAKE-FROM-REAL-IMAG" op))))
  dispatch)

The corresponding
apply-generic
procedure, which applies a
generic operation to an argument, now simply feeds the operation's
name to the data object and lets the object do the work:
⁴⁸

(define (apply-generic op arg) (arg op))

Note that the value returned by
make-from-real-imag
is a
procedure – the internal
dispatch
procedure. This is the
procedure that is invoked when
apply-generic
requests an operation to
be performed.

This style of programming is called
message passing
. The name
comes from the image that a data object is an entity that receives the
requested operation name as a “message.” We have already seen an
example of message passing in section 
2.1.3
, where we saw
how
cons
,
car
, and
cdr
could be defined with no data
objects but only procedures. Here we see that message passing is not
a mathematical trick but a useful technique for organizing systems
with generic operations. In the remainder of this chapter we will
continue to use data-directed programming, rather than message
passing, to discuss generic arithmetic operations. In chapter 3 we
will return to message passing, and we will see that it can be a
powerful tool for structuring simulation programs.

Exercise 2.75.
  
Implement the constructor
make-from-mag-ang
in message-passing style.
This procedure should be analogous to the
make-from-real-imag
procedure given above.

Exercise 2.76.
  
As a large system with generic operations evolves, new types of data
objects or new operations may be needed. For each of the three
strategies – generic operations with explicit dispatch, data-directed
style, and message-passing-style – describe the changes that must be
made to a system in order to add new types or new operations. Which
organization would be most appropriate for a system in which new types
must often be added? Which would be most appropriate for a system in
which new operations must often be added?

In the previous section, we saw how to design systems in which data
objects can be represented in more than one way. The key idea is to
link the code that specifies the data operations to the several
representations by means of generic interface procedures. Now we will
see how to use this same idea not only to define operations that are
generic over different representations but also to define operations
that are generic over different kinds of arguments. We have already
seen several different packages of arithmetic operations: the primitive
arithmetic (
+
,
-
,
*
,
/
) built into our
language, the rational-number arithmetic (
add-rat
,
sub-rat
,
mul-rat
,
div-rat
) of
section 
2.1.1
, and the complex-number arithmetic that we
implemented in section 
2.4.3
. We will now use
data-directed techniques to construct a package of arithmetic
operations that incorporates all the arithmetic packages we have already
constructed.

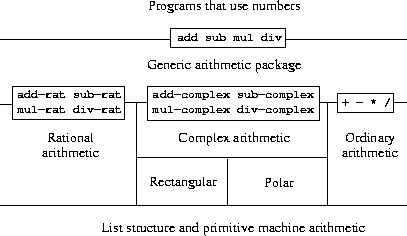
Figure 
2.23
shows the structure of the system we
shall build. Notice the
abstraction barriers. From the perspective
of someone using “numbers,” there is a single procedure
add
that operates on whatever numbers are supplied.
Add
is part of
a generic interface that allows the separate ordinary-arithmetic,
rational-arithmetic, and complex-arithmetic packages to be accessed
uniformly by programs that use numbers. Any individual arithmetic
package (such as the complex package) may itself be accessed through
generic procedures (such as
add-complex
) that combine packages
designed for different representations (such as rectangular and
polar). Moreover, the structure of the system is additive, so
that one can design the individual arithmetic packages separately and
combine them to produce a generic arithmetic system.

Figure 2.23:
  Generic arithmetic system.

The task of designing generic arithmetic operations is analogous to
that of designing the generic complex-number operations. We would
like, for instance, to have a generic addition procedure
add
that
acts like ordinary primitive addition
+
on ordinary numbers,
like
add-rat
on rational numbers, and like
add-complex
on
complex numbers. We can implement
add
, and the other generic
arithmetic operations, by following the same strategy we used in
section 
2.4.3
to implement the generic selectors for
complex numbers. We will attach a type tag to each kind of
number and cause the generic procedure to dispatch to an appropriate
package according to the data type of its arguments.

The generic arithmetic procedures are defined as follows:

(define (add x y) (apply-generic 'add x y))
(define (sub x y) (apply-generic 'sub x y))
(define (mul x y) (apply-generic 'mul x y))
(define (div x y) (apply-generic 'div x y))

We begin by installing a package for handling
ordinary
numbers,
that is, the primitive numbers of our language. We will tag these
with the symbol
scheme-number
. The arithmetic operations in this
package are the primitive arithmetic procedures (so there is no need to
define extra procedures to handle the untagged numbers). Since
these operations each take two arguments, they are installed in the
table keyed by the list
(scheme-number scheme-number)
:

(define (install-scheme-number-package)
  (define (tag x)
    (attach-tag 'scheme-number x))    
  (put 'add '(scheme-number scheme-number)
       (lambda (x y) (tag (+ x y))))
  (put 'sub '(scheme-number scheme-number)
       (lambda (x y) (tag (- x y))))
  (put 'mul '(scheme-number scheme-number)
       (lambda (x y) (tag (* x y))))
  (put 'div '(scheme-number scheme-number)
       (lambda (x y) (tag (/ x y))))
  (put 'make 'scheme-number
       (lambda (x) (tag x)))
  'done)

Users of the Scheme-number package
will create (tagged) ordinary numbers by means of the procedure:

(define (make-scheme-number n)
  ((get 'make 'scheme-number) n))

Now that the framework of the generic arithmetic system is in place,
we can readily include new kinds of numbers. Here is a package that
performs rational arithmetic. Notice that, as a benefit of
additivity, we can use without modification the rational-number code
from section 
2.1.1
as the internal procedures in the
package: