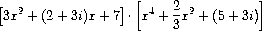Structure and Interpretation of Computer Programs (41 page)

Exercise 2.86.
  Suppose we want to handle complex numbers whose real
parts, imaginary parts, magnitudes, and angles can be either ordinary
numbers, rational numbers, or other numbers we might wish to add to
the system. Describe and implement the changes to the system needed
to accommodate this. You will have to define operations such as
sine
and
cosine
that are generic over ordinary numbers and
rational numbers.

The manipulation of symbolic algebraic expressions is a complex
process that illustrates many of the hardest problems that occur in
the design of large-scale systems. An algebraic expression, in
general, can be viewed as a hierarchical structure, a tree of
operators applied to operands. We can construct algebraic expressions
by starting with a set of primitive objects, such as constants and
variables, and combining these by means of algebraic operators, such
as addition and multiplication. As in other languages, we form
abstractions that enable us to refer to compound objects in simple
terms. Typical abstractions in symbolic algebra are ideas such as
linear combination, polynomial, rational function, or trigonometric
function. We can regard these as compound “types,” which are often
useful for directing the processing of expressions. For example, we
could describe the expression

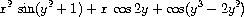
as a polynomial in
x
with coefficients that are trigonometric
functions of polynomials in
y
whose coefficients are integers.

We will not attempt to develop a complete algebraic-manipulation
system here. Such systems are exceedingly complex programs, embodying
deep algebraic knowledge and elegant algorithms. What we will do is
look at a simple but important part of algebraic manipulation: the
arithmetic of polynomials. We will illustrate the kinds of decisions
the designer of such a system faces, and how to apply the ideas of
abstract data and generic operations to help organize this effort.

Our first task in designing a system for performing arithmetic on
polynomials is to decide just what a polynomial is. Polynomials are
normally defined relative to certain variables (the
indeterminates
of the polynomial). For simplicity, we will restrict
ourselves to polynomials having just one indeterminate (
univariate polynomials
).
⁵⁴
We will define a polynomial to be a
sum of terms, each of which is either a coefficient, a power of the
indeterminate, or a product of a coefficient and a power of the
indeterminate. A coefficient is defined as an algebraic expression
that is not dependent upon the indeterminate of the polynomial. For
example,

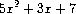
is a simple polynomial in
x
, and

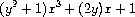
is a polynomial in
x
whose coefficients are polynomials in
y
.

Already we are skirting some thorny issues. Is the first of these
polynomials the same as the polynomial 5
y
²
+ 3
y
+ 7, or not? A
reasonable answer might be “yes, if we are considering a polynomial
purely as a mathematical function, but no, if we are considering a
polynomial to be a syntactic form.” The second polynomial is
algebraically equivalent to a polynomial in
y
whose coefficients are
polynomials in
x
. Should our system recognize this, or not?
Furthermore, there are other ways to represent a polynomial – for
example, as a product of factors, or (for a univariate polynomial) as
the set of roots, or as a listing of the values of the polynomial at a
specified set of points.
⁵⁵
We can finesse these questions by deciding that in our
algebraic-manipulation system a “polynomial” will be a
particular syntactic form, not its underlying mathematical meaning.

Now we must consider how to go about doing arithmetic on polynomials.
In this simple system, we will consider only addition and
multiplication. Moreover, we will insist that two polynomials to be
combined must have the same indeterminate.

We will approach the design of our system by following the familiar
discipline of data abstraction. We will represent polynomials using a
data structure called a
poly
, which consists of a variable and a
collection of terms. We assume that we have selectors
variable
and
term-list
that extract those parts from a poly and
a constructor
make-poly
that assembles a
poly from a given variable and a term list.
A variable will be just a symbol, so we can use the
same-variable?
procedure of section 
2.3.2
to compare variables.
The following procedures define addition and multiplication of polys:

(define (add-poly p1 p2)
  (if (same-variable? (variable p1) (variable p2))
      (make-poly (variable p1)
                 (add-terms (term-list p1)
                            (term-list p2)))
      (error "Polys not in same var -- ADD-POLY"
             (list p1 p2))))
(define (mul-poly p1 p2)
  (if (same-variable? (variable p1) (variable p2))
      (make-poly (variable p1)
                 (mul-terms (term-list p1)
                            (term-list p2)))
      (error "Polys not in same var -- MUL-POLY"
             (list p1 p2))))

To incorporate polynomials into our generic arithmetic system, we need
to supply them with type tags. We'll use the tag
polynomial
,
and install appropriate operations on tagged polynomials in
the operation table. We'll embed all our code
in an installation procedure for the polynomial package,
similar to the ones in
section 
2.5.1
:

(define (install-polynomial-package)
  
;; internal procedures
  
;; representation of poly
  (define (make-poly variable term-list)
    (cons variable term-list))
  (define (variable p) (car p))
  (define (term-list p) (cdr p))
  <
procedures 
same-variable?
 and 
variable?
 from section 
2.3.2
>
  
;; representation of terms and term lists
  <
procedures 
adjoin-term 
...
coeff
 from text below
>
  
;; continued on next page
  (define (add-poly p1 p2) 
...
)
  <
procedures used by 
add-poly
>
  (define (mul-poly p1 p2) 
...
)
  <
procedures used by 
mul-poly
>
  
;; interface to rest of the system
  (define (tag p) (attach-tag 'polynomial p))
  (put 'add '(polynomial polynomial) 
       (lambda (p1 p2) (tag (add-poly p1 p2))))
  (put 'mul '(polynomial polynomial) 
       (lambda (p1 p2) (tag (mul-poly p1 p2))))
  (put 'make 'polynomial
       (lambda (var terms) (tag (make-poly var terms))))
  'done)

Polynomial addition is performed termwise. Terms of the same order
(i.e., with the same power of the indeterminate) must be combined.
This is done by forming a new term of the same order whose coefficient
is the sum of the coefficients of the addends. Terms in one addend
for which there are no terms of the same order in the other addend are
simply accumulated into the sum polynomial being constructed.

In order to manipulate term lists, we will assume that we have a
constructor
the-empty-termlist
that returns an empty term list
and a constructor
adjoin-term
that adjoins a new term to a term
list. We will also assume that we have a predicate
empty-termlist?
that tells if a given term list is empty, a selector
first-term
that extracts the highest-order term from a term
list, and a selector
rest-terms
that returns all but the highest-order
term. To manipulate terms, we will suppose that we have a
constructor
make-term
that constructs a term with given
order and coefficient, and selectors
order
and
coeff
that return, respectively, the order and the
coefficient of the term. These operations allow us to consider both
terms and term lists as data abstractions, whose concrete
representations we can worry about separately.

Here is the procedure that constructs the term list for the sum of two
polynomials:
⁵⁶

(define (add-terms L1 L2)
  (cond ((empty-termlist? L1) L2)
        ((empty-termlist? L2) L1)
        (else
         (let ((t1 (first-term L1)) (t2 (first-term L2)))
           (cond ((> (order t1) (order t2))
                  (adjoin-term
                   t1 (add-terms (rest-terms L1) L2)))
                 ((< (order t1) (order t2))
                  (adjoin-term
                   t2 (add-terms L1 (rest-terms L2))))
                 (else
                  (adjoin-term
                   (make-term (order t1)
                              (add (coeff t1) (coeff t2)))
                   (add-terms (rest-terms L1)
                              (rest-terms L2)))))))))

The most important point to note here is that we used the generic
addition procedure
add
to add together the coefficients of the
terms being combined. This has powerful consequences, as we will see
below.

In order to multiply two term lists, we multiply each term of the
first list by all the terms of the other list, repeatedly using
mul-term-by-all-terms
, which multiplies a given term by
all terms in a given term list. The resulting term lists (one for
each term of the first list) are accumulated into a sum. Multiplying
two terms forms a term whose order is the sum of the orders of the
factors and whose coefficient is the product of the coefficients of
the factors:

(define (mul-terms L1 L2)
  (if (empty-termlist? L1)
      (the-empty-termlist)
      (add-terms (mul-term-by-all-terms (first-term L1) L2)
                 (mul-terms (rest-terms L1) L2))))
(define (mul-term-by-all-terms t1 L)
  (if (empty-termlist? L)
      (the-empty-termlist)
      (let ((t2 (first-term L)))
        (adjoin-term
         (make-term (+ (order t1) (order t2))
                    (mul (coeff t1) (coeff t2)))
         (mul-term-by-all-terms t1 (rest-terms L))))))

This is really all there is to polynomial addition and multiplication.
Notice that, since we operate on terms using the generic procedures
add
and
mul
, our polynomial package is automatically able
to handle any type of coefficient that is known about by the generic
arithmetic package. If we include a
coercion mechanism such as one of
those discussed in section 
2.5.2
,
then we also are automatically able to handle operations on
polynomials of different coefficient types, such as