Structure and Interpretation of Computer Programs (55 page)

Exercise 3.30.
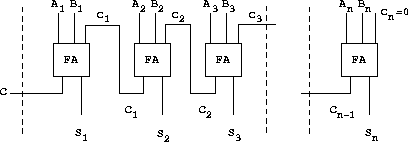
  Figure 
3.27
shows a
ripple-carry adder
formed by stringing
together
n
full-adders. This is the simplest form of parallel adder
for adding two
n
-bit binary numbers. The inputs A
₁
, A
₂
,
A
₃
,
...
, A
_n
and B
₁
, B
₂
, B
₃
,
...
,
B
_n
are the two binary numbers to be added (each A
_k
and B
_k
is a 0 or a 1). The circuit generates S
₁
, S
₂
, S
₃
,
...
, S
_n
, the
n
bits of the sum, and C, the carry from
the addition. Write a procedure
ripple-carry-adder
that
generates this circuit. The procedure should take as arguments three
lists of
n
wires each – the A
_k
, the B
_k
, and the S
_k
– and
also another wire C. The major drawback of the ripple-carry adder is
the need to wait for the carry signals to propagate. What is the
delay needed to obtain the complete output from an
n
-bit
ripple-carry adder, expressed in terms of the delays for and-gates,
or-gates, and inverters?

Figure 3.27:
  A ripple-carry adder for
n
-bit numbers.

A wire in our simulation will be a computational object with two local
state variables: a
signal-value
(initially taken to be 0) and a
collection of
action-procedures
to be run when the signal
changes value. We implement the wire, using message-passing style, as
a collection of local procedures together with a
dispatch
procedure that selects the appropriate local operation, just as we did
with the simple bank-account object in section
 
3.1.1
:

(define (make-wire)
  (let ((signal-value 0) (action-procedures '()))
    (define (set-my-signal! new-value)
      (if (not (= signal-value new-value))
          (begin (set! signal-value new-value)
                 (call-each action-procedures))
          'done))
    (define (accept-action-procedure! proc)
      (set! action-procedures (cons proc action-procedures))
      (proc))
    (define (dispatch m)
      (cond ((eq? m 'get-signal) signal-value)
            ((eq? m 'set-signal!) set-my-signal!)
            ((eq? m 'add-action!) accept-action-procedure!)
            (else (error "Unknown operation -- WIRE" m))))
    dispatch))

The local procedure
set-my-signal!
tests whether the new signal
value changes the signal on the wire. If so, it runs each of the
action procedures, using the following procedure
call-each
,
which calls each of the items in a list of no-argument procedures:

(define (call-each procedures)
  (if (null? procedures)
      'done
      (begin
        ((car procedures))
        (call-each (cdr procedures)))))

The local procedure
accept-action-procedure!
adds the given
procedure to the list of procedures to be run, and then runs the new
procedure once. (See exercise 
3.31
.)

With the local
dispatch
procedure set up as specified, we can
provide the following procedures to access the local operations on
wires:
²⁷

(define (get-signal wire)
  (wire 'get-signal))
(define (set-signal! wire new-value)
  ((wire 'set-signal!) new-value))
(define (add-action! wire action-procedure)
  ((wire 'add-action!) action-procedure))

Wires, which have time-varying signals and may be incrementally
attached to devices, are typical of mutable objects. We have modeled
them as procedures with local state variables that are modified by
assignment. When a new wire is created, a new set of state variables
is allocated (by the
let
expression in
make-wire
) and a
new
dispatch
procedure is constructed and returned, capturing
the environment with the new state variables.

The wires are shared among the various devices that have been
connected to them. Thus, a change made by an interaction with one
device will affect all the other devices attached to the wire. The
wire communicates the change to its neighbors by calling the action
procedures provided to it when the connections were established.

The only thing needed to complete the simulator is
after-delay
.
The idea here is that we maintain a data structure, called an
agenda
, that contains a schedule of things to do. The following
operations are defined for agendas:

• (make-agenda)
  returns a new empty agenda.
  
• (empty-agenda? <
  agenda
  >)
  is true if the specified agenda is empty.
  
• (first-agenda-item <
  agenda
  >)
  returns the first item on the agenda.
  
• (remove-first-agenda-item! <
  agenda
  >)
  modifies the agenda by removing the first item.
  
• (add-to-agenda! <
  time
  > <
  action
  > <
  agenda
  >)
  modifies the agenda by adding the given action procedure to be run at
  the specified time.
  
• (current-time <
  agenda
  >)
  returns the current simulation time.
  

The particular agenda that we use is denoted by
the-agenda
. The procedure
after-delay
adds new
elements to
the-agenda
:

(define (after-delay delay action)
  (add-to-agenda! (+ delay (current-time the-agenda))
                  action
                  the-agenda))

The simulation is driven by the procedure
propagate
, which
operates on
the-agenda
, executing each procedure on the agenda
in sequence. In general, as the simulation runs, new items will be
added to the agenda, and
propagate
will continue the simulation
as long as there are items on the agenda:

(define (propagate)
  (if (empty-agenda? the-agenda)
      'done
      (let ((first-item (first-agenda-item the-agenda)))
        (first-item)
        (remove-first-agenda-item! the-agenda)
        (propagate))))

The following procedure, which places a “probe” on a wire, shows the
simulator in action. The probe tells the wire that, whenever its
signal changes value, it should print the new signal value, together
with the current time and a name that identifies the wire:

(define (probe name wire)
  (add-action! wire
               (lambda ()        
                 (newline)
                 (display name)
                 (display " ")
                 (display (current-time the-agenda))
                 (display "  New-value = ")
                 (display (get-signal wire)))))

We begin by initializing the agenda and specifying delays for the
primitive function boxes:

(define the-agenda (make-agenda))
(define inverter-delay 2)
(define and-gate-delay 3)
(define or-gate-delay 5)

Now we define four wires, placing probes on two of them:

(define input-1 (make-wire))
(define input-2 (make-wire))
(define sum (make-wire))
(define carry (make-wire))
(probe 'sum sum)
sum 0  New-value = 0
(probe 'carry carry)
carry 0  New-value = 0

Next we connect the wires in a half-adder circuit (as in
figure 
3.25
), set the signal on
input-1
to 1,
and run the simulation:

(half-adder input-1 input-2 sum carry)
ok
(set-signal! input-1 1)
done
(propagate)
sum 8  New-value = 1
done

The
sum
signal changes to 1 at time 8. We are now eight time
units from the beginning of the simulation. At this point, we can set
the signal on
input-2
to 1 and allow the values to propagate:

(set-signal! input-2 1)
done
(propagate)
carry 11  New-value = 1
sum 16  New-value = 0
done

The
carry
changes to 1 at time 11 and the
sum
changes to 0
at time 16.

Exercise 3.31.
  
The internal procedure
accept-action-procedure!
defined in
make-wire
specifies that when a new action procedure is added to
a wire, the procedure is immediately run. Explain why this initialization
is necessary. In particular, trace through the half-adder example in
the paragraphs above and say how the system's response would differ if
we had defined
accept-action-procedure!
as

(define (accept-action-procedure! proc)
  (set! action-procedures (cons proc action-procedures)))

Finally, we give details of the agenda data structure, which holds the
procedures that are scheduled for future execution.

The agenda is made up of
time segments
. Each time segment is a
pair consisting of a number (the time) and a
queue (see
exercise 
3.32
) that holds the procedures that are
scheduled to be run during that time segment.

(define (make-time-segment time queue)
  (cons time queue))
(define (segment-time s) (car s))
(define (segment-queue s) (cdr s))

We will operate on the time-segment queues using the queue operations
described in section 
3.3.2
.

The agenda itself is a one-dimensional table of time segments. It
differs from the tables described in section 
3.3.3
in that
the segments will be sorted in order of increasing time. In addition,
we store the
current time
(i.e., the time of the last action
that was processed) at the head of the agenda. A newly constructed
agenda has no time segments and has a current time of 0:
²⁸

(define (make-agenda) (list 0))
(define (current-time agenda) (car agenda))
(define (set-current-time! agenda time)
  (set-car! agenda time))
(define (segments agenda) (cdr agenda))
(define (set-segments! agenda segments)
  (set-cdr! agenda segments))
(define (first-segment agenda) (car (segments agenda)))
(define (rest-segments agenda) (cdr (segments agenda)))

An agenda is empty if it has no time segments:

(define (empty-agenda? agenda)
  (null? (segments agenda)))

To add an action to an agenda, we first check if the agenda is empty.
If so, we create a time segment for the action and install this in
the agenda. Otherwise, we scan the agenda, examining the time of each
segment. If we find a segment for our appointed time, we add the
action to the associated queue. If we reach a time later than the one
to which we are appointed, we insert a new time segment into the
agenda just before it. If we reach the end of the agenda, we must
create a new time segment at the end.

(define (add-to-agenda! time action agenda)
  (define (belongs-before? segments)
    (or (null? segments)
        (< time (segment-time (car segments)))))
  (define (make-new-time-segment time action)
    (let ((q (make-queue)))
      (insert-queue! q action)
      (make-time-segment time q)))
  (define (add-to-segments! segments)
    (if (= (segment-time (car segments)) time)
        (insert-queue! (segment-queue (car segments))
                       action)
        (let ((rest (cdr segments)))
          (if (belongs-before? rest)
              (set-cdr!
               segments
               (cons (make-new-time-segment time action)
                     (cdr segments)))
              (add-to-segments! rest)))))
  (let ((segments (segments agenda)))
    (if (belongs-before? segments)
        (set-segments!
         agenda
         (cons (make-new-time-segment time action)
               segments))
        (add-to-segments! segments))))

The procedure that removes the first item from the agenda deletes the
item at the front of the queue in the first time segment. If this
deletion makes the time segment empty, we remove it from the list of
segments:
²⁹

(define (remove-first-agenda-item! agenda)
  (let ((q (segment-queue (first-segment agenda))))
    (delete-queue! q)
    (if (empty-queue? q)
        (set-segments! agenda (rest-segments agenda)))))

The first agenda item is found at the head of the queue in the first
time segment. Whenever we extract an item, we also update the current
time:
³⁰