Structure and Interpretation of Computer Programs (90 page)

which leads to

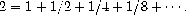
However, if we try the same manipulation beginning with the
observation that - 1 is the solution to the equation
y
= 1 + 2
y
, we
obtain

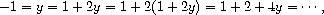
which leads to

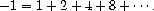
Although the formal manipulations used in deriving these two equations
are identical, the first result is a valid assertion about infinite
series but the second is not. Similarly, for our unification results,
reasoning with an arbitrary syntactically constructed expression may
lead to errors.

⁸¹
Most Lisp systems give the user the ability to
modify the ordinary
read
procedure to perform such
transformations by defining
reader macro characters
. Quoted
expressions are already handled in this way: The reader automatically
translates
'expression
into
(quote expression)
before the
evaluator sees it. We could arrange for
?expression
to be
transformed into
(? expression)
in the same way; however, for
the sake of clarity we have included the transformation procedure here
explicitly.

Expand-question-mark
and
contract-question-mark
use
several procedures with
string
in their names.
These are Scheme primitives.

Computing with Register Machines

We began this book by studying processes and by describing processes
in terms of procedures written in Lisp. To explain the meanings of
these procedures, we used a succession of models of evaluation: the
substitution model of chapter 1, the environment model of chapter 3,
and the metacircular evaluator of chapter 4. Our examination of the
metacircular evaluator, in particular, dispelled much of the mystery
of how Lisp-like languages are interpreted.
But even the metacircular evaluator leaves important questions
unanswered, because it fails to elucidate the mechanisms of control in
a Lisp system. For instance, the evaluator does not explain how the
evaluation of a subexpression manages to return a value to the
expression that uses this value, nor does the evaluator explain how
some recursive procedures generate iterative processes (that is, are evaluated
using constant space) whereas other recursive procedures generate recursive
processes. These questions remain unanswered because the metacircular
evaluator is itself a Lisp program and hence inherits the control
structure of the underlying Lisp system. In order to provide a more
complete description of the control structure of the Lisp evaluator,
we must work at a more primitive level than Lisp itself.

In this chapter we will describe processes in terms of the step-by-step
operation of a traditional computer. Such a computer, or
register
machine
, sequentially executes
instructions
that
manipulate the contents of a fixed set of storage elements called
registers
. A typical register-machine instruction applies a
primitive operation to the contents of some registers and assigns the
result to another register. Our descriptions of processes executed by
register machines will look very much like “machine-language”
programs for traditional computers. However, instead of focusing on
the machine language of any particular computer, we will examine
several Lisp procedures and design a specific register machine to
execute each procedure. Thus, we will approach our task from the
perspective of a hardware architect rather than that of a
machine-language computer programmer. In designing register machines,
we will develop mechanisms for implementing important programming
constructs such as recursion. We will also present a language for
describing designs for register machines. In
section 
5.2
we will
implement a Lisp program that
uses these descriptions to simulate the machines we design.

Most of the primitive operations of our register machines are very
simple. For example, an operation might add the numbers fetched from
two registers, producing a result to be stored into a third register.
Such an operation can be performed by easily described hardware. In
order to deal with list structure, however, we will also use the
memory operations
car
,
cdr
, and
cons
, which require
an elaborate storage-allocation mechanism. In
section 
5.3
we study their implementation in
terms of more elementary operations.

In section 
5.4
, after we have accumulated experience
formulating simple procedures as register machines, we will design a
machine that carries out the algorithm described by the metacircular
evaluator of section 
4.1
. This will fill in the gap in
our understanding of how Scheme expressions are interpreted, by
providing an explicit model for the mechanisms of control in the
evaluator.
In section 
5.5
we will study a simple compiler that
translates Scheme programs into sequences of instructions that can be
executed directly with the registers and operations of the evaluator
register machine.

To design a register machine, we must design its
data paths
(registers and operations) and the
controller
that sequences
these operations. To illustrate the design of a simple register
machine, let us examine Euclid's Algorithm, which is used to compute
the greatest common divisor (GCD) of two integers. As we saw in
section 
1.2.5
, Euclid's Algorithm can be carried out by an iterative
process, as specified by the following procedure:

(define (gcd a b)
  (if (= b 0)
      a
      (gcd b (remainder a b))))

A machine to carry out this algorithm must keep track of two numbers,
a
and
b
, so let us assume that these numbers are stored in two
registers with those names. The basic operations required are testing
whether the contents of register
b
is zero and computing the
remainder of the contents of register
a
divided by the contents
of register
b
. The remainder operation is a complex process,
but assume for the moment that we have a primitive device that
computes remainders. On each cycle of the GCD algorithm, the contents
of register
a
must be replaced by the contents of register
b
, and the contents of
b
must be replaced by the remainder of
the old contents of
a
divided by the old contents of
b
.
It would be convenient if these replacements could be done
simultaneously, but in our model of register machines we will assume
that only one register can be assigned a new value at each step. To
accomplish the replacements, our machine will use a third
“temporary” register, which we call
t
. (First the remainder
will be placed in
t
, then the contents of
b
will be placed
in
a
, and finally the remainder stored in
t
will be placed
in
b
.)

We can illustrate the registers and operations required for this
machine by using the data-path diagram shown in
figure 
5.1
. In this
diagram, the registers (
a
,
b
, and
t
) are represented
by rectangles. Each way to assign a value to a register is
indicated by an arrow with an
X
behind the head, pointing from
the source of data to the register. We can think of the
X
as a
button that, when pushed, allows the value at the source to “flow”
into the designated register. The label next to each button is the
name we will use to refer to the button. The names are arbitrary, and
can be chosen to have mnemonic value (for example,
a<-b
denotes
pushing the button that assigns the contents of register
b
to
register
a
). The source of data for a register can be another
register (as in the
a<-b
assignment), an operation result (as in
the
t<-r
assignment), or a constant (a built-in value that
cannot be changed, represented in a data-path diagram by a triangle
containing the constant).

An operation that computes a value from constants and the contents
of registers is represented in a data-path diagram by a trapezoid
containing a name for the operation. For example, the box marked
rem
in figure 
5.1
represents an
operation that computes the remainder of the contents of the
registers
a
and
b
to which it is attached. Arrows
(without buttons) point from the input registers and constants to the
box, and arrows connect the operation's output value to registers.
A test is represented by a circle containing a name for the test. For
example, our GCD machine has an operation that
tests whether the contents of register
b
is zero. A test also has arrows from its input
registers and constants, but it has no output
arrows; its value is used by the controller rather than by the data
paths. Overall, the data-path diagram shows the registers and
operations that are required for the machine and how they must be
connected. If we view the arrows as wires and the
X
buttons as
switches, the data-path diagram is very like the wiring diagram for a
machine that could be constructed from electrical components.

Figure 5.1:
  Data paths for a GCD machine.