The Unimaginable Mathematics of Borges' Library of Babel (18 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

Since the size of the proton
is approximately 10
15
, we set these two terms equal to each other
and then simplify the equation.
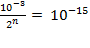 , which implies
, which implies 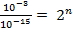 ;
;
therefore,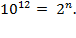
Solving this last equation
without logarithms would be very difficult. (In fact, in 2004, powerful
mathematical software running on my late-model computer crashed the computer in
a failed, naïve, brute-force attempt to solve for such an
n
.) Since 10
12
and 2
n
, although written differently, are the same number, it should
again be the case that any function applied to both of them will output the
same number. Thus,
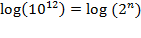 ,
,
which, by using the remarkable
property of the logarithm, entails that
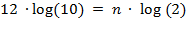 .
.
Dividing both sides by log(2)
yields
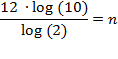
which can quickly be solved
with a computer, a calculator, or—for traditionalists—logarithm tables. When we
do so, we find that
n
is about equal to 39.9, so to ensure we get the
result we want, we round upwards. Thus, if we cut the initial page's thickness
in half 40 times, it will be the case that the 41st page is thinner than a proton.
Topology and Cosmology
The Universe (which Others
Call the Library)
A fact is the end or last
issue of spirit. The visible creation is the terminus or the circumference of
the invisible world.
—Ralph
Waldo Emerson, "Nature"
 TOPOLOGY IS A BRANCH OF MATHEMATICS THAT
TOPOLOGY IS A BRANCH OF MATHEMATICS THAT
explores properties and invariants of spaces, and for the purposes
of this book we consider a space to be a set of points unified by a
description. Cosmology is quite literally the study of our cosmos. If we
consider the Library to constitute a universe and the universe to be the
Library, it is not unreasonable to combine these notions and speculate as to a
conceivable topology of the Library that best reflects the anonymous
librarian's received wisdom and secret hopes.
Early in the
story—and many commentators have noted the connection between the italicized
phrase and Borges' essay "Pascal's Sphere"— Borges writes
Let it
suffice for the moment that I repeat the classic dictum:
The Library is a
sphere whose exact center is any hexagon and whose circumference is
unattainable.
The final sentences of the
story invite us to reopen the question of the topology of the Library:
I am perhaps
misled by old age and fear, but I suspect that the human species—the only human
species—teeters at the verge of extinction, yet that the Library—enlightened,
solitary, infinite,
perfectly unmoving, armed with
precious volumes, pointless, incorruptible, and secret—will endure.
I have just written the word "infinite." I have not
included that adjective of out of mere rhetorical habit; I hereby state that it
is not illogical to think that the world is infinite. Those who believe it to
have limits hypothesize that in some remote place or places the corridors and
stairs and hexagons may, inconceivably, end—which is absurd. And yet those who
picture the world as unlimited forget that the number of possible books is
not.
I will be bold enough to suggest this solution to the ancient problem:
The Library is unlimited but periodic.
If an eternal voyager should journey
it in any direction, he would find after untold centuries that the same volumes
are repeated in the same disorder—which, repeated, becomes order: the Order. My
solitude is cheered by that elegant hope.
Collecting the properties of
the classic dictum (CD) and the Librarian's solution (LS), we obtain the
following list:
1. Spherical
(CD)
2. Center
can be anywhere—uniform symmetry (CD)
3. Circumference
is
unattainable.
(CD)
4. No
boundaries (LS)
5.
Limitless
(LS)
6. Periodic
(LS)
Is there a space that embodies
all six of these properties? If so, how can we best envision it and grasp it
with our intellect? We claim there is an excellent candidate that encompasses
these properties, if we are willing to refine our interpretations just a
smidge. In the Math Aftermath to this chapter, we discuss two other compelling
ways ofconfiguring the Library that each significantly expand our conceptions
of the possible.
Let's begin
with the space most familiar to our intuitive geometric sense: Euclidean
three-dimensional space (henceforth,
3-space).
It is a space we think of
as possessing volume, as having three axes of orientation with ourselves as the
central point; we may move forward or backwards, we may move left or right, and
we may move up or down. And, ofcourse, we may also move in combinations of
these directions. Notice that from this description, there is no fixed
preferred center point:
we are our own central points.
Indeed, one
of Descartes' deepest ideas was to specify a point—some point, any point—in
3-space and call it the origin. Three axes intersecting at the origin,
typically called the x, y, and
z
axes, are set with each axis at right
angles to the other two. They abstract our innate, intuitive orientation and,
with the introduction of a unit length, which naturally induces a numbering of
the axes, give rise to a coordinatization of space. Algebra can now conjoin
geometry, creating analytic geometry, and later spawn calculus.
But there
are no distinguished points of any kind in Euclidean 3-space; in fact, the view
from any point is the same as from any other point. There are no walls, no
boundaries, and no limits. It seems at the end of the story the librarian
envisioned this kind of space, partitioned into hexagons, filled with books,
extending infinitely throughout the totality of 3-space. The books' shelving
pattern repeats endlessly along each of the three axes, much as a symmetric
wallpaper pattern does in two dimensions. While this conception of the Library
satisfies points 2, 4, 5, and 6, it also induces a vertiginous disorientation
born of trying to imagine a thing extending away forever. For example, if the
Library goes
down
forever, what do the hexagons rest on? More hexagons?
Rather remarkably, the architectural, model of the Library that we propose
provides a satisfying answer to this question.