The Unimaginable Mathematics of Borges' Library of Babel (16 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

Following
the example set by the equation, choose the first page to be one-half of a
standard page's thickness, then the next page half that thickness, the next
half that thickness, and so on and so on. Then the entire Book, infinitely
periodically repetitive, will be exactly one standard page thickness.
In the Math
Aftermath following the chapter, we provide a bit more background on this next
calculation, which is estimating the thickness of the 41st page. We conclude
that the 41st page is


which
is thinner than the diameter of a proton. Since each successive page is
one-half the thickness of the preceding page, all the rest of the pages are
also thinner than a proton. Of course, in this interpretation, though almost
every page is invisible to the naked eye, or even an electron microscope,
it
is not the case that any page is actually "infinitely thin."
Here, we take "infinitely
thin" in the sense indicated by the reference to Cavalieri's principle in
the footnote: the thickness of a Euclidean plane. The thickness of a plane is
the same as the length of a point, which is tricky to define. Consider a point
in the line. It is clear that a Euclidean point is thinner than a line segment
of
any
positive length. It is somewhat disquieting, though, to say that
a point has length 0; if so, how does massing together sufficiently many
0-length entities create a line of positive length? Doesn't adding together 0s
always produce another 0? How could an object be of length 0?
A subtle way
of evading these traps was crafted at the beginning of the twentieth century,
primarily through the work of Henri Lebesgue, whose theory is now a vast
edifice with ramifications permeating much of modern mathematics. Fortunately,
we need only a small cornerstone of the theory: the idea of a set of measure 0
contained in the
real number line.
Recall that
the real number line consists of all rational and irrational numbers, each
representing a point on the line, each also signifying the distance from the
origin to the point. It may be confusing that we are explicitly identifying the
"length of an interval" with a "number," for again, a
real-world idea, that of length, is interpenetrating a mathematical
idealization. We inhabit this limbo for the rest of the chapter.
We need two
definitions. A
closed interval
includes both endpoints of an interval;
as an example, the notation [0, 1] means "all numbers between 0 and 1,
inclusive." Now, let
S
be any set contained in the real number line. One says that
S
is
a set of measure 0
if
S
can be
contained in a union, possibly infinite, of closed intervals whose lengths add
up to an arbitrarily small number. Several examples will help clarify this
definition.

Example 1.
A single point
p
in the real number line. Clearly
p
can be contained in a closed interval of arbitrarily small length (figure 6).
Thus
p
is a set of measure 0. Note the fine distinction: we are not
saying "the point
p
is of length 0"; rather we are saying that
p
is a set whose measure is 0. It turns out—and we'll see an example
soon—that there are sets of measure 0 which are quite counterintuitive.
Example 2.
Three points
a
,
b
, and
c
in the real number
line. Let
a
be contained in an interval of length 1/2,
b
be contained in an interval of length 1/4, and
c
be contained in an interval of length 1/8.
(It doesn't matter if the
intervals overlap.) Then the three points are contained in a union of intervals
whose sum-length is
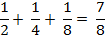
Not arbitrarily small yet! But
now, let
a
be contained in an interval of length 1/4,
b
be contained in an interval of length 1/8, and
c
be contained in an interval of length 1/16.
Then, since each interval is
half the length of its corresponding predecessor, the sum is also halved.
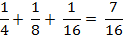

If we play this game again,
starting with an interval of length 1/8, we find that
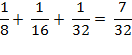
If we continue to put
a
,
b
, and
c
in intervals half of the lengths of the previous go-round,
the triple of intervals will also sum to half the preceding length: first 7/64,
then 7/128, and so on. By starting with a sufficiently small interval, we
ensure the sum of the three intervals is arbitrarily small—that is, the set
S
= {
a ,b ,c
} is a set
of measure 0 (figure 7).
Example 3.
It is a curious fact that it is difficult to show that the
interval of numbers between 1 and 4 is
not
of measure 0. Certainly our
intuition informs us that the minimum length of intervals necessary to cover
[1, 4] will sum to 3, but demonstrating it rigorously is a nontrivial exercise,
well beyond the scope of this book. See figure 8.
