The Unimaginable Mathematics of Borges' Library of Babel (15 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

Now, if there are an odd
number of primes in the list, the median is the absolute middle of the list. If
there are an even number of primes in the list, the median is the average of
the two primes appearing in the middle of the list. (The average of these two
numbers is guaranteed to be an integer, for the sum of two odd numbers is even,
and we conclude the calculation of the average by dividing by two.)
The only way
to find the median would be, in one way or another, to account for the complete
list of prime numbers expressible in 100 digits. Including 0, there are exactly
one googol numbers expressible in 100 digits. By the famous prime number
theorem—which we'll outline in a moment—there are more than 10
97
prime numbers smaller than 10
100
. This number may sound manageable,
but 10
97
is trillions of times larger than the number of subatomic
particles in our universe. There simply isn't any imaginable way to list and
keep track of 10
97
numbers, which precludes the possibility of
finding the median.
1
The prime
number theorem was first conjectured in various forms by Euler and others
beginning in the late eighteenth century and was finally proved about a hundred
years later in 1896 by Hadamard (and independently that same year by Poussin).
Part of the beauty of the prime number theorem is that it provides an excellent
estimate of how many primes there are that are smaller than 10
100
without explicitly naming a single one!
The prime
number theorem says that if n
(n
) is equal to "the number of primes
less than or equal to n," then as
n
grows very large,
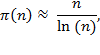
where ln(
n
) is the
natural log function. (The natural log has the same remarkable properties as
the log function, log(
n
), that we looked at
earlier, and indeed, after multiplication by a constant, they are the same
function.) We are interested in knowing approximately the number of primes
expressible in 100 digits, so we compute
π
(10
100
) for a good
estimate:
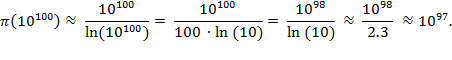
Real Analysis
The Book of Sand
To see a World in a Grain
of Sand
And a Heaven in a Wild
Flower
Hold Infinity in the palm
of your hand
And Eternity in an hour.
—William
Blake, "Auguries of Innocence"
 REAL ANALYSIS IS THE BRANCH
REAL ANALYSIS IS THE BRANCH
OF MATHEMATICS
that explores, among other
ideas, the nuances of the arbitrarily small. Paradoxically, in this chapter,
thinking about the very small will prove decisive in understanding the very
large: the Book that embodies the entire Library.
Borges' last
insight regarding the Library is cloaked in a footnote adorning the conclusion
of the last sentence. The footnote reads:
Letizia Álvarez
de Toledo has observed that the vast Library is pointless; strictly speaking,
all that is required is
a single volume,
of the common size, printed in
nine- or ten-point type, that would consist of an infinite number of infinitely
thin pages. (In the early seventeenth century, Cavalieri said that every solid
body is the superposition of an infinite number of planes.) Using that silken
vademecum
would not be easy: each apparent page would open into other similar pages; the
inconceivable middle page would have no "back."
Others have independently
noticed that Borges continued to play with the idea of such a Book in his
evocative short story "The Book of Sand."
1
The
mathematical analysis of a Book of Sand hinges on what is meant by the phrase
"infinitely thin pages." Three different interpretations of
"infinitely thin" lead to three Books similar in spirit, but
disparate in the details. We'll examine them in ascending order of exoticness.
Interpretation
If we take "infinitely
thin" to mean merely "thinner than any subatomic particle,"
there are several refreshing possibilities. First, there are (410) (25
(25
1,312,000
) pages in the Library, a very large
number, but still finite. Thus, if every page is the same thickness, say
 th
th
of an inch,
then the Book, sans cover,
will be exactly one inch thick. Such a Book, though, would defraud the
anonymous librarian of his "elegant hope" that the Library is
repeated in its disorder, and also contravene the explicit statement in the
footnote that the book would consist of an infinite number of pages. If, as
above, the pages were all the same thickness, then an infinite periodic
repetition of all the books of the Library would force the Book of Sand to be
infinitely thick.
If we insist
on each page having a definite thickness, and we equally insist upon infinite
repetitions for the pages of the Book, we must therefore allow for ever-thinner
pages. To make sense of such a Book, we need to understand an idea from the
theory of infinite sums.
2
We'll begin this short journey by treading parallel to the tiny
footfalls, echoing loudly through the ages, of the Paradox of Zeno so beloved
by Borges.
Suppose,
starting at one end of a room, we were to walk halfway across towards the
opposite wall. After a brief pause, we walk half the distance from the midpoint
towards the opposite wall. After another brief pause, we walk half the distance
.. . (see figure 5).
In the
coarse world we inhabit, we'll stub our toes on the wall in short order. In the
idealized world of mathematics, we may always halve the distance between one
point and an endpoint. (Zeno's and Parmenides' paradoxes exploit this chasm
between the world of our perceptions and the mathematical vision of a line
segment.)

For the purposes of this book,
without offering a rigorous proof, note that by adding up the lengths
symbolized by the arcs, the information encoded in figure 5 is equivalent to
this equation:
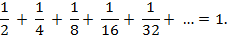
This equation encapsulates a
striking fact: by adding up infinitely many segments, each smaller than the
previous by one-half, a form of unity is achieved. A gauge of the depth and
profundity of this insight is that for several centuries, most thinkers
conceded that this hammered home the final nail in the coffin for Zeno's
Paradox. (Nowadays, thinkers have again complexified the picture, thereby casting
doubt, raising questions, and essentially resurrecting the dead.)