The Unimaginable Mathematics of Borges' Library of Babel (12 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

This
amenable collection of books is designed to enable
Books in English
to
include a title and short accurate description of the contents. This nearly
accomplishes the first half of the task of a catalogue; although the books
aren't uniquely specified, the scope of possibility is greatly constricted.
However, the other half of a catalogue, that of specifying a location, is also
fraught with difficulties.
First, and
most strongly emphasized by Borges, is the apparent lack of organization in the
distribution of books. It is possible that there is an overarching pattern, but
even ifthere is, it would be impossible to deduce it from local information.
The librarian's "elegant hope" that the Library is (truly) infinite
and periodic would provide a godlike observer with a kind of an order for each
book; every particular book would have an infinite number of exact copies—unimaginably
distant from each other— and these infinite copies would constitute a set of
regularly spaced three-dimensional lattice points. But this pattern does not
serve our needs.
Finite or
infinite, the problem of identifying individual hexagons of the Library is
insurmountable. If the Library is a 3-sphere or any of the other spaces
described in the chapter "Topology and Cosmology," the number of
hexagons is finite. However, since each hexagon holds 640 books, which is
approximately 25
2,007
books, more than 25
1,311,997
(approximately
10
1,834,095
) hexagons are required to hold all the Library's books.
This means that if one were to attempt to write out a number for each hexagon
in our familiar base-10 notation, it would take 1,834,095
digits.
Now
each book in the Library has exactly 1,312,000 slots to fill, and, moreover,
the orthographic symbols contain no (recognizable) digits. Writing a number out
in words usually uses many more precious slots; for example,
[one
million, eight hundred thirty four thousand, and ninety five] versus 1,834,095.
The bracketed expression takes
63 spaces, while the second needs only nine. For almost every hexagon in the
Library, a volume of a hypothetical
Books in English
catalogue could not
actually contain the corresponding hexagon number where a book is shelved.
Trying to
circumvent this problem, one may observe that many numbers have shorter
expressions, such as 2
4,781
, and legitimately wonder if
every
integer might have a remarkably condensed form. An insuperable problem is that
there are many such condensed expressions, including the one above, that need a
computer to calculate. More disturbing, though, is an example of a condensed
verbal description of a "small" number— only 100 digits—that even we,
using networked supercomputers, would be unable to find:
The
median
of the prime numbers expressible in 100 digits.
Thus, even
if the catalogue entry for the
Tractatus Logico-Philosophicus
listed the
location as
Hexagon: the
median of the prime numbers expressible in one hundred digits.
Shelf: four.
Position:
seventeen.
the information is as useless
to us as it is to a librarian. (See the Math Aftermath "Numb and Number
(Theory)" for more discussion about prime numbers and, in particular, why
we are unable to determine the median of the prime numbers expressible in 100
digits.)
Usually,
outside of computer science, we use
base
10 to represent the positive
integers, meaning we use the 10 symbols {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} to label
numbers. In these circumstances, though, one might try using a higher base than
10 for the integers, such as base 25, to number the hexagons. There are two
problems associated with this: first, it would still take all but two slots of
a book to list a hexagon number, which suffices to invalidate the usefulness.
Second, since each book contains only 25 orthographic symbols, each such symbol
would have to stand for a digit. So, if one were to write out the hexagon
number in base-25 digits, it would usually look like complete gibberish. (In
fact, it also leads to an unpleasant, yet valid, interpretation of the Library:
it is the complete listing of all base-25 numbers comprised of exactly
1,312,000 digits.) At any rate, such a book would not be "recognizably
English"; thus it would not itself be listed in
Books in English.
What if,
like Ireneo Funes, from Borges' celebrated short story "Funes the
Memorious," we resolved to work in base 24,000? It would do no good: in
the story, for each number up to 24,000 Funes created his own signifier, for
example, names such as
Brimstone, Clubs,
and
The Whale.
In the
Library, we are stuck with 25 orthographic symbols. Instead of combining 10
digits in various ways to fill five places to make a number between 1 and
24,000, we would need to combine the 25 symbols in a minimum of four places to
distinguish 24,000 separate numbers, because
25
4
=
390,625
while
25
3
=
15,625
which doesn't provide enough
distinct signifiers to take us up to base 24,000. Anyway, not only wouldn't
this convention save much space, it also leads back to the previous dilemma:
writing out the names of the numbers will result in waterfalls of gibberish.
Finally, a
potential catalogue entry might take a different tack. It might give
coordinates, such as, "Go up ninety-seven floors, move diagonally left
four thousand hexagons, and then move diagonally right another two hundred and
twenty." Although this might, at first blush, seem appealing, the same
sorts of problems arise, for most hexagons are unimaginably far away. The
example provided above works simply because the numbers involved—97, 4,000, and
220—are so miniscule, so accessible. The Library is neither.
The
Library is its own catalogue. Any other catalogue is unthinkable.
Math
Aftermath: Numb and Number (Theory)
A metaphysician is one who,
when you remark that twice two makes four, demands to know what you mean by
twice, what by two, what by makes, and what by four. For asking such questions
metaphysicians are supported in oriental luxury in the universities, and
respected as educated and intelligent men.
—H.
L. Mencken,
A Mencken Chrestomathy
Below are two outgrowths from
the sprawling yet spare field of number theory; together they form a pair of
relatively straightforward mathematical confections. Both revolve around using
prime numbers decisively to reach interesting conclusions.
Consider the
25
1,312,000
distinct volumes in the Library: a simple rethinking of
this number will produce a result surely unimagined by Borges. Now, as we all
know, the number 25
factors
into 5 5, so
5, so
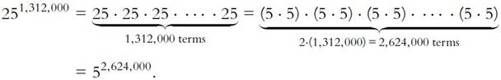
A
prime number
is a
positive integer greater than one that is divisible only by itself and by one.
The unique factorization theorem, proved by Euclid in
The Elements,
says
that every positive integer is decomposable into exactly one
product
of
primes, each of which is raised to a power greater than or equal to one. For
example, we all know that 100 = 10 10, and it's also true that 100 = 4
10, and it's also true that 100 = 4 25. So, what is 100 equal to, 10
25. So, what is 100 equal to, 10 10 or 4
10 or 4 25? Of course you're laughing at us, because 100 is obviously
25? Of course you're laughing at us, because 100 is obviously
equal to both products. Neither of these answers, though, is written exactly as
a product of primes, in which each prime is raised to a power greater than or
equal to one. Based on the two factorizations—10 10 and 4
10 and 4 25—it's easy to see that
25—it's easy to see that