The Unimaginable Mathematics of Borges' Library of Babel (14 page)

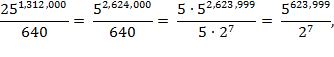
and none of the seven 2s in
the denominator may divide any of the millions of 5s in the numerator. This
means that the books do not exactly fill out all the hexagons, which entails
that either the Library is
not complete
(!!!), or that there is a
special hexagon that is not full, or that at least one hexagon is differently
configured, or that at least one hexagon contains exact copies of other books
in the Library. We can't imagine that Borges considered this—or would have
cared—when he assigned numbers to the quantity of shelves on a wall or the
number of books per shelf in the Library.

Also, it may
seem easy to juggle and tweak the numbers of shelves and books to make each
hexagon hold, say, 625 = 5
⁴
books. After all, as written in the
story, each hexagon holds 640 books, and 625 is very close to 640. But this is
an opportunity to admire the power of Euclid's unique factorization theorem: if
each of the four non-doorway walls has the same number of shelves, and if each
shelf holds the same number of books, then each hexagon must hold

(4 walls)
x
(
m
shelves per wall)
x
(
n
books per shelf) = 4
mn
books.

The prime factors 2
²
= 4 will always be there; neither adjusting the number of shelves per wall, nor
the tally of books per shelf will budge those 2s, which means that 4mn can
never cleanly divide 25
^1,312,000
.

How, then,
might we arrange matters so that the total number of distinct volumes may be
evenly distributed throughout the hexagons? One possible solution is to expand
the alphabet to 25 letters and, as Borges did, include the space, the comma,
and the period to round the total up to 28 = (2
²
)
 7 orthographic symbols. Then, if the other (admittedly
arbitrarily chosen) numbers for each book stay the same, there will be 28
^1,312,000
distinct books.

Next, hire
infinitely many cabinetmakers to rebuild the bookshelves in the hexagons, so
that each of the four walls holds four shelves, and each shelf holds 49 books.
Then a total of 4
 4
 49 = 784 = (2
⁴
)
 (7
²
) books furnish each hexagon, and since

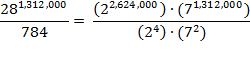
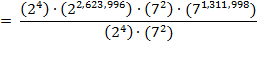
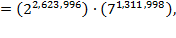
after the renovation, the 28
^1,312,000
books exactly fill (2
^2,623,996
)
(7
^1,311,998
) hexagons.

For this last section, the aim
is to explain concisely why we are currently, and for the foreseeable future,
unequal to the task of determining the median of the prime numbers expressible
in 100 digits. The median of the set of primes expressible in 100 digits is, in
a sense, the "middle" of all of those primes. To compute the median,
arrange the numbers sequentially from the smallest to the largest prime less
than 10
¹⁰⁰
(which is called one googol).