The Unimaginable Mathematics of Borges' Library of Babel (17 page)

Back to the infinitely thin
pages of the Book. We interpret "infinitely thin" as meaning that
each page has a thickness of measure 0. We also assume, as we did at the end of
the first interpretation, that within this Tome, the books of the Library
repeat over and over, enacting the anonymous librarian's "elegant
hope" of a periodically repeating order. We are therefore confronted with
an intriguing problem:

There are
infinitely many pages, each of which has thickness of measure 0. How thick is    
the Book?

The answer might run counter
to your intuition:

The
thickness of the Book is of measure 0.

In other words, if we looked
at the Book sideways, we would not be able to see it, let alone open it. How
does this unexpected, unimagined, unimaginable state of affairs arise? Once we
think to look for it, it turns out to be sitting there, almost as if it was
waiting to be discovered.

The goal is
to show that the thickness of the Book can be contained in a collection of
closed intervals which can be chosen so that the sum of their lengths can be
made arbitrarily small. If this can be done, then by definition the Book is of
measure 0. We'll accomplish this by covering the thickness of each page in
ever-smaller intervals in a sneaky way that exploits the infinite sum that
embodied Zeno's Paradox.

First,
though, another counterintuitive point, followed by a technical one. Although
it's conceivable that the Bookbinder bound the infinitely many pages of the
Book together in a straightforward order, it is also possible that the pages of
the Book wash up against themselves similar to the
rational numbers,
meaning there is no more a "first" page of the Book than there is a
"first" positive rational number. If so, we simply choose one of the
25
^1,312,000
books to be the first, another to be the second, and so
on, until we have a complete list of the books and their pages. Since the Book
repeats, we are thus able to give numbers to its pages.
³
So, let

the first
page be contained in an interval of length 1/2,

the second
page be contained in an interval of length 1/4,

the third
page be contained in an interval of length 1/8,

and so on,

and so on.

We saw in the first
interpretation that

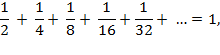
so the thickness of the Book
can contained in an infinite union of intervals which sum to 1. Here's where
the sneaky part comes in. Now, let

the first
page be contained in an interval of length 1/4,

the second
page be contained in an interval of length 1/8,

the third
page be contained in an interval of length 1/16,

and so on,

and so on.

This time, the infinite union
of intervals sums to

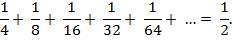
This is seen by simply
subtracting 1/2 from both sides of the previous equation. Notice how we are
exploiting an aspect of the idea of infinity: we are throwing away a term from
the left side of the equation, but still have infinitely many terms to account
for the infinite number of pages.

If we start
by letting the thickness of the first page be contained in an interval of
length 1/8, then the sum becomes:

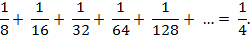
Clearly, by continuing to play
this game of lopping the intervals in half, we ensure that we may always find a
union of intervals that contains the thickness of the Book and sums to an
arbitrarily small number. This means that the thickness of the Book is of
measure 0, an outcome surely unimagined by Borges.

How it is
possible to create a line segment, a set of positive measure, out of points of
measure 0? That is a long story for another day.

Perhaps the elusive nature of
the preceding interpretation is unsatisfying; we never took a stand on how
thick "infinitely thin" is; we merely observed that it is of measure
0. For the third interpretation, we will glimpse some of the basic elements of
one of the most underutilized mathematical theories of the twentieth century:
nonstandard analysis. The roots of the development of nonstandard analysis
began with Leibniz, one of the inventors of the calculus. Both Leibniz and
Newton used infinitely small quantities,
infinitesimals
(also known as
fluxions),
in their early calculations. In his foreword to the revised
edition of Abraham Robinson's seminal work,
Non-standard Analysis,
the
logician Wilhelmus Luxemburg notes that "Bishop Berkeley disdainfully
referred to infinitesimals as the 'ghosts of departed quantities,"' and
that in response to this and other attacks, "Leibniz proposed a program to
conceive of a system of numbers that would include infinitesimally small as
well as infinitely large numbers."

Because of
the difficulties inherent in beginning Leibniz's bold program, and for other
historical reasons, his ideas lay fallow for almost 300 years. In 1961, with
the publication of
Non-standard Analysis,
Robinson rebutted Berkeley and
fulfilled Leibniz's dream. Using various tools of logic and set theory
developed in the late nineteenth and early twentieth centuries, Robinson was
able to create a consistent, logical model of a number system that included
infinitesimals.

It should be
mentioned, with sincere respect, that adherents of non-standard analysis
possess a striking combination of mystic fervor and matter-of-fact pragmatism
about the topic. This may be because the mainstream of mathematics has, at
least for now, marginalized nonstandard analysis due to its less intuitive
constructions and technical complexities. Bearing this in mind, here are
selections, originally excerpted by Mark McKinzie and Curtis Tuckey, from H.
Jerome Keisler's college textbook, which approaches the calculus from the
nonstandard viewpoint (emphases added by present author).

In grade
school and high school mathematics, the real number system is constructed
gradually in several stages. Beginning with the positive integers, the systems
of integers, rational numbers and finally real numbers are built up . . .

What is needed [for an understanding of the calculus] is a sharp
distinction between numbers which are small enough to be neglected and numbers
which aren't. Actually, no real number except zero is small enough to be
neglected.
To get around this difficulty, we take the bold step of
introducing a new kind of number, which is infinitely small and yet not equal
to zero . . .

The real line is a subset of the hyperreal line; that is, each
real number belongs to the set of hyperreal numbers. Surrounding each real
number
r
, we introduce a collection of hyperreal numbers infinitely
close to
r
.
The hyperreal numbers infinitely close to zero are called
infinitesimals.
The reciprocals of nonzero infinitesimals are infinite
hyperreal numbers. The collection of all hyperreal numbers satisfies the same
algebraic laws as the real numbers . . .

We have no way of knowing what a line in physical space is
really like. It might be like the hyperreal line, the real line, or neither.
However, in applications of the calculus it is helpful to imagine
a line in physical space as a hyperreal line. The hyperreal line is, like the
real line, a useful mathematical model for a line in physical space.

In nonstandard analysis, there
are infinitely many hyperreal infinitesimals clustered around 0, every one
smaller than any positive real number. Each signifies an infinitely small
distance. We may simply assign any infinitesimal we wish to each page of the
Book.
⁴
By the rules of nonstandard analysis, we compute the
thickness of the Book by adding together all of the infinitesimals. For a
summation such as this one, adding the infinite number of infinitesimals
produces yet another infinitesimal, so the Book is, again, infinitely thin:
never to be seen, never to be found, never to be opened. This time, though, we
may elegantly console ourselves that the infinite thinness is a precisely
calculable nonstandard thickness.

Regardless of which
interpretation we assume, if the pages are 'infinitely thin,' then by necessity
the Book of Sand itself is infinitely thin.

Math
Aftermath: Logarithms Redux

Reason looks at necessity
as the basis of the world; reason is able to turn chance in your favor and use
it. Only by having reason remain strong and unshakable can we be called a god
of the earth.

—Johann
Wolfgang Von Goethe,
Wilhelm Meister's
Apprenticeship,
bk. I, ch. 17

Recall that in the first Math
Aftermath, we used logarithms to solve an equation involving exponentials. This
is another example, only slightly more complicated, of using logarithms to
solve an equation. Earlier in this chapter, we claimed that if the Book of Sand
started with a normal page thickness, say one millimeter, 10
^-3
meters, and each successive page was half the thickness of the preceding page,
then the 41st page would be thinner than a proton, which measures a little more
than 10
^-15
meters across. How did we find the number 40?

Let's set it
up as an equation. Each page is half the thickness of the preceding page, so if
we measure the
n
th page after the first page, it will be the thickness
of the first page cut in half
n
times. That is, it will be

 meters across.