The Unimaginable Mathematics of Borges' Library of Babel (34 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

If we remind
ourselves of the work we did in the chapter "Combinatorics," we see
that the number of books containing the story
at a specific starting
position
is the number of different ways the slots not occupied by the
story can be filled. The number of unfilled slots is

From the first paragraph of
this note, we see there are 1,294,001 such positions; thus there are
approximately
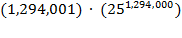
distinct books in the Library
containing the story. So the probability of finding a Library volume containing
the story is
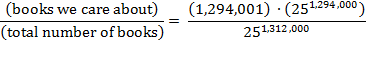

which, in turn, is
approximately
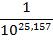
This is roughly equivalent to
the likelihood of winning a major lottery 3,600 times in succession!
There is,
however, a profound sense in which Hayles is correct, a sense that Borges
explicitly intended. You
are
in the Library. A multivolume set is
scattered throughout the Library that details every single day of your life,
including your death. In fact, a multi-quintillion volume set that details the
lives, deaths, and protein transfers of each and every one of your cells is
also scattered throughout the Library.
By invoking
this theme in conjunction with the idea of potential inaccuracies of a
particular volume, Hayles opens the door to a stimulating line of thought.
Suppose, miraculously, you were to find a grouped set of volumes, each of which
had one page dedicated to one day of your life. Every single page, as far as
your memory can recall and corroborate, is an accurate portrayal of that day.
You read the page that corresponds to
tomorrow.
At the end of the next
day, you reread the page: it, too, turns out to be an accurate description of the
day. You continue this process for years; unimaginably, and despite your
perverse and whimsical attempts to subvert their accuracy, the books continue
to meticulously depict your days.
Here's the
question: can you now say, with certainty, that the page that corresponds to
today's tomorrow will also be accurate? No! Based on the number of books in the
Library and the number of ways in which the description may be inaccurate,
despite the long streak of accurate descriptions, it is almost a certainty that
the book will deviate. This is a disturbing and counterintuitive conjunction of
probability with the comprehensiveness of the Library, yet it is unavoidable.
Perhaps this example might help clarify the point. Suppose you flipped a fair
coin 15,000 times, which is about once a day for 40 years, and it always came
up heads. If you flipped the coin tomorrow, would you expect it to be heads or
tails? Of course you'd expect it to be heads again—but if it's a fair coin,
there's an equally likely chance it will be tails! A closer correspondence to
the probabilities associated with such a book might be: suppose that every day
for the past 20 years, you've won the big jackpot of the daily lottery Do you
believe you'll win tomorrow, too? The odds are tremendously against it, but
then again, the odds were even more incredible against your winning every day
for 20 years. How can you rationally assess tomorrow?

Merrell's book,
Unthinking
Thinking: Jorge Luis Borges, Mathematics, and the New Physics,
is the most
comprehensive attempt to link ideas of modern mathematics, physics, and
philosophy with Borges, via the critical tools of literary analysis. As such,
Unthinking Thinking
contains a number of interesting insights and
juxtapositions. For example, Merrell offers unique perspectives on the
structure of the Library as seen through the lenses of the theory of special
relativity and the expanding universe theory
I think
Merrell makes solid contributions in two areas. I particularly enjoyed his
thoughts regarding enantiomorphic (mirror-reversed) forms. He provides a nice
discussion of mirror-reversal in the Möbius band and applies his notion
imaginatively to the "problem" of mirrors in the Library, especially
in reference to his relativistic "world-lines" of librarians.
Second,
Merrell gives four arguments for the impossibility of deriving a global order
of the Library from the local information that a librarian would have
available. Merrell's arguments run the gamut from intertextual references to
Borges' story "Averroes' Search" to an appeal to authorities on
probability; in particular, Spencer-Brown and the astronomer Layzer, as quoted
in Campbell.
Here is a
concrete way of thinking about this problem. Suppose I provide you with a rule
to generate a sequence, something such as "Start with the two numbers 0,
1. Forever after, employ Rule Fib."
Rule Fib:
The next number in the sequence is defined to be the sum of the preceding two
numbers.
Rule Fib entails that to find
the third number, you must add the first two numbers:
0,
1, 0 + 1 = 0, 1, 1.
To get the fourth number, you
add the second and third terms, 1 + 1, and get:
0, 1, 1, 2.
To get the fifth number, you
add the third and fourth terms, 1 + 2, and get:
0, 1, 1, 2, 3.
The sequence—actually a famous
sequence, known as the
Fibonacci sequence
—begins to grow rapidly:
0,
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,...
Given time and inclination,
you or a computer could generate many numbers of this sequence. Conversely, if
I provided you with the sequence above, you might well guess the rule that
produces "the next term." However, the rule might be much more
complicated; for example, it might be: "Let the first 12 terms correspond
to the Fibonacci sequence; let the next 12 be the first 12 digits in the decimal
expansion of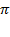 ; the 47 digits after that should all be 7s; etc. etc. etc."
; the 47 digits after that should all be 7s; etc. etc. etc."
Given a more complicated rule such as this last one, although your guess is
"good," it relies on the false assumption that the rule generating
the sequence must be as simple
as possible. This has
the unfortunate effect that your good guess produces the wrong answer. I
conclude that without complete information, there is no way to ensure the
successful induction of a
unique
generating-rule for a sequence.
