The Unimaginable Mathematics of Borges' Library of Babel (10 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

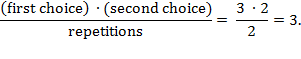
Another way to think about
repetitions is as the number of distinct orderings of, for instance, a set of
k
objects. There is a critical difference between this and the exponential
work from earlier in the chapter; when calculating the number of books, we
allowed an orthographic symbol to be used over and over and over again—possibly
1,312,000 times. Or, conversely, a symbol didn't need to appear at all. In an
ordering, every object needs to appear exactly once. In the beginning of the
chapter "More Combinatorics," we show how to calculate the number of
distinct orderings of a set of
k
objects: it's a product of
k
integers, notated
k!
and
pronounced "k factorial." For now, suffice it to note that

This explains the denominator
of the formula: we divide out by all the repetitions given by all the different
orderings of the
k
chosen objects and thus achieve a masterpiece of the
ars combinatorial:
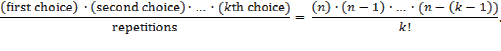
Applying this formula to the
situation of choosing subsets of size 16 from a set of size 1,312,000 yields
the expression
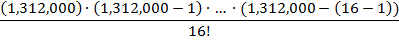
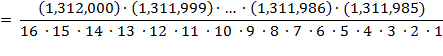
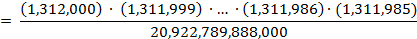
=
3,683,681,259,485,362,310,918,865,543,989,208,654,728,931,149,486,911,733,618,072,454,576,141,229,488,660,718,000

 .
.
·
167652204904152536250654781631104887775960706846318297081203114099863966650917588689423169009077773845740905744085778827320617721109316599473995687145914975458247961380758354211972797797543235764905722567864684228003984140011308404044321592205678736478798197529921801160919630700034601028770571338599864608382013346981059927132254573497776678238401077140182956790820433072855508726888278875670104566601988133173085774616250929807519759554422254267977193932033675325750012118425565945197783300697670477973441801403529924202599494700263231670373218710201565540800286289853720350162893048473231040579020269713422436208955186831616206109715328190796442616740197330756096397254259481411179297605714105015291757369390571424809705710527995642620280697196621430275793093225927800376559882994925327612689196008920829563638966405968151079193703516798977935410410870485480473180206692696460141319574750537162302401458151912894683905017520492915492610250607658200820459233579973871624581533039027827192594822076477326080909994846009681777529003361408645173508147190013663404830519365501647324846666372695454023369419855605974124635054913613707789078539963199486512143281891270633487234820460978516962245945218404332537360951568826338781616551557083534695665518111841590380729315478105653632803123719714062985622464780873761799170525539055256885813059255491913245295763000439144465356103197575576731159299217928919322435311018790938012446381695777636352
Information Theory
Cataloging the Collection
It is a very sad thing that
nowadays there is so little useless information.
—Oscar
Wilde, "A Few Maxims for the Instruction of the Over-Educated"
 INFORMATION THEORY IS ONE
INFORMATION THEORY IS ONE
OF THE YOUNGEST
fields in mathematics,
essentially born in 1948 when Claude Shannon published "A Mathematical
Theory of Communication." As a discipline, it is still unfolding, still
crystallizing into a way to analyze and interpret the world. For the purposes
of this book, we'll say that information theory is the study of the compression
and communication of complex information. We consider each book in the Library
to be a complex piece of information, and our inquiry takes the form of
investigating how a catalogue of the Library might encode information about the
content and location of books. Since the story was written while Borges was
tasked with cataloguing the collection of the Miguel Cane Municipal Library,
questions of this nature may have taken on rich significance for him.
Typically, a
library catalogue card, either physical or virtual, contains two distinct kinds
of information. The first sort uniquely specifies a book in such a way that a
reader with partial or incomplete information still might identify the book: a
title, author, edition, publisher, city of publication, year of publication,
and short description of the contents generally appear on a card and prove
sufficient. An ISBN also uniquely specifies a book, but probably isn't much use
in finding a book if we remember only a few digits of the number.
The second
type of information uniquely specifies a location in the library, although
additional knowledge is usually required. For example, under most systems of
cataloguing currently in use, the call numbers, in addition to uniquely
specifying a book, include an abundance of letters and digits, often
interspersed with decimal points. If one does not know, say, where the PQ books
are shelved, the information is degraded. Even if the books were arranged
alphabetically by author or title, for a large collection we'd still need to
know in what general region to begin our search. By analogy, many dictionaries
have thumbnail indentations which enable readers quickly to find a section of
words beginning with one or several letters. Both of these categories of
information are problematic for the Library of Babel.