The Unimaginable Mathematics of Borges' Library of Babel (6 page)

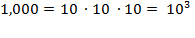
distinct ways to fill the
three slots. By seizing on these ideas, by sensing that a simple pattern has
been established and can be used to predict what we couldn't possibly list, we
may ask how many distinct ways there are to fill, for example, 36 slots, where
each slot contains one of our 10 allowed orthographic symbols and repetition of
symbols is allowed. By applying the reasoning we established above, we see that
there must be 10
³⁶
ways; that is, a 1 followed by thirty-six 0s—a
thousand billion, billion, billion, billion, billion, billion ways:

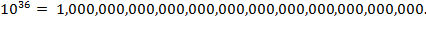
Just for a lark, here are the
first few and last few slot-fillings of the usual way one would list the
fillings.

1.
     
000000000000000000000000000000000000

2.
     
000000000000000000000000000000000001

3.
     
000000000000000000000000000000000002

 (Quite a few more!)

(10
³⁶
– 2).
99999999999999999999999999999999997

(10
³⁶
– 1).
99999999999999999999999999999999998

10
³⁶
.
99999999999999999999999999999999999

And that's the end of the
list.

In an article in the academic
journal
Variaciones Borges,
our ideal reader, Umberto Eco, argues that
the exact number of distinct volumes in the Library is irrelevant to both the
story and to the reader. To the extent that the numbers of pages, lines, and
letters in each book were chosen arbitrarily by Borges, we agree with him. (See
the beginning of the chapter "Geometry and Graph Theory" for a quote
from Borges regarding this matter.) However, we assert that understanding the
combinatorial process that produces the exact number of distinct volumes is
both important and relevant to an understanding of the story So let's apply
these ideas to the story and, given the numbers and constraints Borges
provides, use them to calculate the number of distinct volumes in the Library.

In "The
Library of Babel," Borges writes:

...each book
contains four hundred ten pages; each page, forty lines; each line,
approximately eighty black letters. There are also letters on the front cover
of each book; these letters neither indicate nor prefigure what the pages
inside will say.

From these lines, we conclude
each book consists of 410
 40
 80 = 1,312,000 orthographic symbols; that is, we may consider a
book as consisting of 1,312,000 slots to be filled with orthographic symbols.
Here a few more excerpts from the next few paragraphs:

There are
twenty-five orthographic symbols.
That discovery
enabled mankind, three hundred years ago, to formulate a general theory ofthe
Library and thereby satisfactorily resolve the riddle that no conjecture had
been able to divine—the formless and chaotic nature of virtually all books.. .

Some five hundred years ago, the chief of one of the upper
hexagons came across a book as jumbled as all the others, but containing almost
two pages of homogeneous lines. He showed his find to a traveling decipherer,
who told him the lines were written in Portuguese; others said it was Yiddish.
Within the century experts had determined what the language actually was: a
Samoyed-Lithuanian dialect of Guarani, with inflections from classical Arabic.
The content was also determined: the rudiments of combinatory analysis,
illustrated with examples of endlessly repeating variations. These examples
allowed a librarian of genius to discover the fundamental law of the Library.

This philosopher observed that all books, however different from
one another they might be, consist of identical elements: the space, the
period, the comma, and the twenty-two letters of the alphabet. He also posited
a fact which all travelers have since confirmed:
In all the Library, there
are no two identical books.
From those incontrovertible premises, the
librarian deduced that the Library is "total"—perfect, complete, and
whole—and that its bookshelves contain all possible combinations of the
twenty-two orthographic symbols (a number which, though unimaginably vast, is
not infinite)—that is, all that is able to be expressed, in every language.

How many distinct books
constitute the Library? Each book has 1,312,000 slots, each of which may be
filled with 25 orthographic symbols—this is the "variations with unlimited
repetition" mentioned above. Again, by employing the ideas outlined above,
there are

25 ways to
fill one slot,

25
 25 = 25
²
ways to fill two slots,

25
 25
 25 = 25
³
ways to fill three slots,

and so on,

and so on
for 1,312,000 slots.

It follows immediately that
there are

25
^1,312,000

distinct books in the Library
That's it.

Somehow, it
feels all too easy, even anticlimactic, as though instead we should have had to
write pages and pages of dense, technical, high-level mathematics, overcoming
one complex puzzle after another, before arriving at the answer. But most of
the beauty—the elegance—of mathematics is this: applying potent ideas and clean
notation to a problem much as the precise taps of a diamond-cutter cleave and
husk the dispensable parts of the crystal, ultimately revealing the fire
within. (Perhaps we should have ended the calculation by writing "That's
it!" instead of "That's it.")