The Unimaginable Mathematics of Borges' Library of Babel (9 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

By using a calculator, a
computer, or even Henry Brigg's log tables from 1617, we find
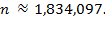
Therefore,
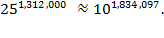
Math
Aftermath II: An Example of the Ars Combinatoria
Drawing is a struggle
between nature and the artist, in which the better the artist understands the
intentions of nature, the more easily he will triumph over it. For him it is
not a question of copying, but of interpreting in a simpler and more luminous
language.
—Charles
Baudelaire,
The Salon of 1846,
VII. "On the Ideal and the Model"
In the final analysis, a
drawing simply is no longer a drawing, no matter how self-sufficient its
execution may be. It is a symbol, and the more profoundly the imaginary lines
ofprojection meet higher dimensions, the better.
—Paul
Klee,
The Diaries of Paul Klee 1898-1918,
no. 681, entry for July 1905
Here, we endeavor to explain
the origins of the (possibly) mysterious formulas appearing earlier in the
chapter. The first one arises in the context of trying to determine the number
of distinct books in the Library consisting of 1,311,998 occurrences of the
letter
g
and two instances of the letter
h
.
We abstract
the books and hexagons away from the problem by noting that what we are really
interested in can be characterized as the question "How many distinct ways
exist to pick two objects from 1,312,000?" The two objects, of course,
correspond to the two slots that we will fill with the letter
h
. So, the
number of distinct ways to choose two objects from 1,312,000 corresponds
precisely to the number of distinct books under discussion.
As it turns
out, for millennia combinatorialists have known a formula for this and related
questions; in the most general terms, the number of different ways to choose a
subset of
k
objects from a set of
n
objects is equal to

One way to uncover the
derivation of this formula is to break the analysis into two parts, first
explaining the terms appearing in the numerator, and then understanding the
term in the denominator. (Joe Roberts, the professor who introduced me to
combinatorial analysis, helpfully said "attic" and
"basement" instead of "numerator" and
"denominator.")
We wish to
choose one object from
n
distinct objects. Thus, we have
n
choices for our first object and then we are left with
n
— 1 objects.
So, when we choose the second object, we have
n
— 1 distinct objects to
choose from. This means that choosing
two
objects is tantamount to
having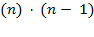 ways to pick them:
ways to pick them:
n
ways to choose the first object
multiplied by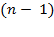 ways to choose the second.
ways to choose the second.
If we pick a
third object, we are choosing from distinct objects, and so the numerator grows accordingly. Notice
distinct objects, and so the numerator grows accordingly. Notice
that when we pick a fourth object, we choose from distinct objects; thus, extending the developing pattern, when we
distinct objects; thus, extending the developing pattern, when we
pick the
k
th object, we are selecting it from the remaining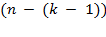 distinct objects. Multiplying, in succession, all of the choices
distinct objects. Multiplying, in succession, all of the choices
yields the numerator (attic):
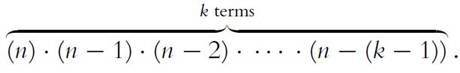
At this
juncture, it's reasonable to wonder why there needs to be a denominator
(basement). Why can't we simply stop at the numerator, or, put another way,
what is wrong with what we've derived? The answer is devilishly simple: there
are a number of different ways to pick the exact same subset of size
k,
and we don't care in what order the
k
objects are chosen. We just want
to know which are the chosen ones.
Let's
illustrate this with an easy example. We have a
set,
a collection, of
three distinct objects, {A, B, C}. Let's choose all
subsets
consisting
of two distinct objects:
{A,
B} {B, A}
{A,
C} {C, A}
{B,
C} {C, B}
If the order in which the
objects are picked is important, then we have a complete list of all subsets of
size two. However, if order is unimportant, then {A, B} and {B, A} are both
names for the same subset. Really, then, we would be happy with, say, this
list.
{A,
B}
{A,
C}
{C,
B}
Since all we care about is the
number of ways to choose two things, and we don't care about the order, we need
to divide out by the number of repetitions, which in this case, is two. We thus
arrive at the complete formula for this example,