The Unimaginable Mathematics of Borges' Library of Babel (22 page)
Read The Unimaginable Mathematics of Borges' Library of Babel Online
Authors: William Goldbloom Bloch
Tags: #Non-Fiction

Because of the impossibility
of aligning the cylinder ends, the Klein bottle cannot live in three
dimensions; it requires at least four. A way of representing it in three
dimensions is depicted in figure 26, but it requires a self-intersection. You
can actually do this nicely by starting with a large enough piece of paper,
marking the sides, taping the top and bottom edges together to make a cylinder,
and then cutting a hole in the side to pass one end of the cylinder through.
This is an excellent way to see how to allow the orienting arrows to point in
the same direction. Perhaps this analogy will help explain why allowing the
Klein bottle to be in four dimensions effaces the self-intersection. Suppose we
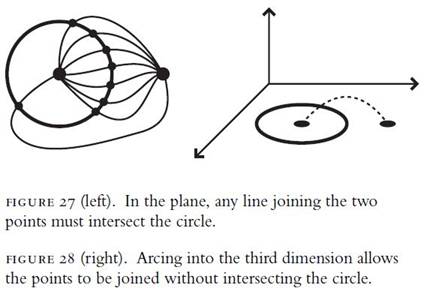
confined ourselves to the two-dimensional Euclidean plane and were interested
in joining a point inside a circle to a point outside the circle by a line
(figure 27). Regardless of devious twists, turns, or serpentine path, it's
pretty obvious that any curve joining the two points must intersect the circle
somewhere.


The only possible way to
connect the points without intersecting the circle is to venture into the third
dimension, pulling a path out of the plane (figure 28). Similarly, one may
eliminate the self-intersection of the Klein bottle by simply pulling the
offending part of the cylinder into the fourth dimension.
The
"twisted" portion of the initial description of the Klein bottle
comes from the fact that one could change the order of the construction by
first identifying the left and right sides of the square before identifying the
top and bottom. To identify the left and right sides, one must twist the
square—and in so doing, create a Mobius band. If we did that, though, at this
juncture it is very difficult to visualize how to glue the top and bottom
together to make the Klein bottle, because the top and bottom have been merged
into one entity, a circle seemingly doubled on itself.
The "disoriented"
portion stems from technical considerations and is manifest in two related, but
distinct, ways. We'll cover them both below.
Suppose we
decide to walk a counterclockwise path on what appears to be the outside of the
Klein bottle. In figure 29, the black arrow pointing out of the surface into
space will represent our position as we start to walk, feet on the Klein
bottle, head in the clouds.
Now some
weighty philosophic problems naturally arise from even this innocent beginning.
Euclid's plane and all 2-manifolds, including the Klein bottle, are
"infinitely thin," much like the pages of the Book of Sand. Is the
Euclidean plane therefore transparent? Does the plane, or any 2-manifold,
possess a distinct "top" and "bottom"? (Borges makes
playful use of these questions in his story "The Disk.") The
mathematical perspective is that a path in the Euclidean plane or on a
2-manifold is simultaneously visible from both sides, and as such, it might be
useful to imagine the Euclidean plane as a thin and supple sheet of transparent
plastic. Then, any line painted on, for example, the top of the plastic is
essentially visually indistinguishable from its image as seen through the
plastic from below.

As we begin our walk along the
surface, our feet naturally remain on the surface, while our heads naturally
are "outside" in 3-space. Next, follow the path to where the two ends
of the cylinder are identified. (This looks like the "hole" at the
front of the Klein bottle in figure 26.) Note that as we enter the
"hole", the arrow and the path both are faded to suggest that we are
now inside the Klein bottle, and that our heads are now pointing "inside"
rather than "outside." Keep moving "inside" the Klein
bottle through the self-intersection—which isn't really there— until we've
circled around to our starting point (figure 29). The arrow representing us was
initially pointing "out" and now it is pointing "in." The
Klein bottle, which has neither holes nor boundaries, also has no inside or
outside in the sense that we intuitively understand these terms— a disorienting
revelation indeed.
A faintly
analogous situation occurs with the familiar circle. In the plane, there's a
distinct inside and outside—look again at figure 27. As discussed earlier in
the chapter, in 3-space the circle has nothing easily definable as an
"inside" or an "outside." It certainly does not cut 3-space
into two eternally separate pieces, as does, for example, a 2-sphere. The
correspondence between the Klein bottle's and the circle's lack of an inside
and an outside hinges on dimensionality. A circle is a one-dimensional object
that can live in two dimensions. If the circle is in the plane, in 2-space,
then the "dimensional difference"—technically, the
codimension
—is
equal to one:
2 - 1 =
dimension(2-space) - dimension(circle) =
1.
On the other hand, if the
circle is in 3-space, the codimension is equal to two:
3 - 1 =
dimension(3-space) - dimension(circle) = 2.
Similarly, if the Klein
bottle, a two-dimensional object, is in 4-space, the codimension is once again
equal to two. A codimension greater than one implies that the object can't
separate the space into two distinct pieces; thus, there can be no inside or
outside.
Summarizing,
the Klein bottle is an example of a
one-sided
2-manifold with no
boundary (By contrast, the Mobius band, another delightfully disorienting
object, has a boundary, an edge.) All the boundaryless 2-manifolds familiar to
us from our sensual life in 3-space have an inside and an outside—think of a
sphere, a torus, the surface of a pretzel, or the surface of any familiar
object. They all cut space into two distinct pieces.
The Klein
bottle does not separate space—it has one side only, and there is no way of
distinguishing between the inside and the outside. Moreover, in
four-dimensional Euclidean space, the Klein bottle is geometrically flat for
the same reasons as the torus: pick any two points on it, reverse the
identifications back to a square, then draw the straight line that connects the
two points. An unimaginable construct, to say the least.
There is another
disorientation involving the Klein bottle. For this one, we imagine, taking a
cue from
Flatland,
that we live a two-dimensional existence
wholly
contained within the surface
of the Klein bottle. Outside and inside are
meaningless words to us: the Klein bottle is our entire universe. Befitting our
new planar existence, let us take a new form, that of a flag rather than an
arrow. The flag that we are curves and bends with the Klein bottle as we move
around; again, it is—we are—wholly contained within the universe that is the
Klein bottle.
Again, this
time the black flag is part of the surface of the Klein bottle, not
perpendicular to the surface like the arrows in the previous illustration. See
figure 30. Now move the flag counterclockwise along a path that exploits the
one-sided nature of the Klein bottle, the same path as in the previous section.
As in figure 29, we change the shade of both the path and the flag as they
proceed from the "outside" of the Klein bottle through the
"hole" to the "inside." Note that throughout our journey,
the black flag points in the direction of motion.
Observe that
although the flag begins its journey with the pole pointing in one direction on
the surface of the Klein bottle, after it has slid around to the starting point
the pole, still contained in the universe that is the Klein bottle, is now
pointing in the other direction. Perhaps, jaded by the one-sided oddity of the
Klein bottle, this isn't a big surprise—after all, it is easy to imagine
slithering around on the floor and ending up with our feet located at their
initial spot and with our head pointed in the opposite direction than at the
start.

More disorienting, though,
the black flag has come back a mirror reflection of itself.
There is no
obvious intuitive analogue for us. Any journey you take, transformative though
it may be, will not result in your coming back as a mirror-reflected image of
yourself. You may, for example, feel a shadow of your former self, or half the
person you used to be, or find your partner besieged by 50 suitors; regardless,
it will not be the case that your heart is now, from everyone else's
perspective, on the right-hand side of your body. Figure 31 illustrates the
categorical difference between a rotation and a mirror-reflection.