The Cosmic Landscape (21 page)

Hubble’s technique for measuring the motion of a galaxy was a familiar one. The light from a galaxy was sent through a spectroscope that breaks it up into its component wavelengths. Isaac Newton, way back in the seventeenth century, did exactly that when he sent white sunlight through a triangular prism. The prism, a simple spectroscope, broke the sunlight into all the colors of the rainbow. Newton concluded, rightly, that sunlight is a composite of red, orange, yellow, green, blue, and violet light. Today, we know that each color of the spectrum corresponds to a wave of a particular (wave)length.

If one looks very carefully at the spectrum of starlight, some extremely narrow dark
spectral lines
can be seen superimposed on the rainbow of colors.

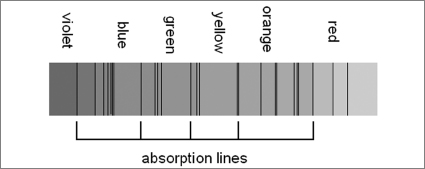
These mysterious lines of missing light are called
absorption lines.
They indicate that something along the line of sight has absorbed certain discrete wavelengths (colors) without disturbing the rest of the spectrum. What causes this curious phenomenon? The quantum mechanical behavior of electrons.

According to Bohr’s original quantum theory of the atom, electrons in atoms move in quantized orbits. Newtonian mechanics would allow the electron to orbit at any distance from the nucleus. But quantum mechanics constrains them to move like motor vehicles that are required, by law, to stay in definite lanes. Being between lanes violates the traffic laws: being between quantized orbits violates the laws of quantum mechanics. Each orbit has its own energy, and for an electron to jump from one orbit to another, the energy of the electron has to change. If an electron jumps from an outer to an inner orbit, it must radiate a photon to carry off the excess energy. Conversely, an inner electron can jump to a more distant orbit only if it gains some energy, possibly by absorbing a photon.

Normally an electron moves in the innermost available orbit that is not blocked by other electrons (remember that the Pauli exclusion principle prevents any two electrons from occupying the same quantum state). But if the atom is struck by another object, an electron can absorb some energy and make a
quantum jump
to a new orbit, one farther from the nucleus. The atom is temporarily
excited,
but eventually the electron will emit a photon and drop back to its original orbit. The light radiated in this way has definite wavelengths that are characteristic of the type of atom. Each individual chemical element has its own signature, a set of spectral lines that corresponds to these quantum jumps.

If a photon of the right color falls on an unexcited atom, the reverse process can happen: the photon can be absorbed while the electron jumps to a more energetic orbit. This has an interesting effect on starlight passing through hydrogen gas in the atmosphere surrounding a star. The hydrogen will deplete the starlight of precisely those colors that characterize the hydrogen spectrum. If helium or carbon or any other element is present, it will also leave its distinguishing mark on the starlight. Studying the spectra of starlight is the way we know about the chemical makeup of stars. But our interest right now is not the chemical composition but rather the velocity of the star. The point is that the exact details of the absorption spectrum, as seen from earth, depend on the relative velocity between us and the star. The key is the Doppler effect.

If you have heard the siren of a police car as it speeds past, then you’ve experienced the Doppler effect. The high-pitched whine, “eeee,” of the approach gives way to the lower sound, “ooo,” as the siren recedes. During the approach the sound waves coming toward you are bunched up, and conversely, while the car moves off, they are stretched out. Because wavelength and frequency are closely related, you hear “eeeeooooo.” You could amuse yourself by trying to estimate how fast the police car is moving by the magnitude of the frequency shift.

But the Doppler effect is not just an amusement for pedestrians. For astronomers it is nothing less than the key to the structure and history of the universe. The Doppler effect happens to all kinds of waves: sound waves, vibrational waves in crystals, even water waves. Try wiggling your finger in the water while hanging off the side of a slowly moving boat.
¹
The ripples spreading out along the direction of motion are bunched up. The ones going in the reverse direction are stretched.

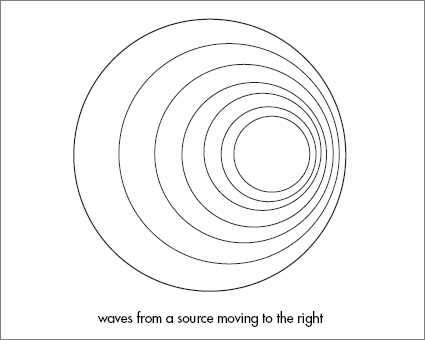
Luckily for astronomers light emitted by a moving object does the same thing. A rocket-propelled lemon moving away from you might have the color of an orange or even a tomato if it were going fast enough.
²
While it’s moving toward you, you might mistake it for a lime or even a giant blueberry. This is because light from sources moving away from the observer is
redshifted
and light from approaching sources is
blueshifted.
This applies just as well to the light from galaxies as from lemons. Moreover, the amount of shift is a measure of the velocity of the galaxy, relative to the earth.

Hubble used this phenomenon to determine the velocity of a large number of galaxies. He took very accurate spectra of the light coming from each galaxy and compared the spectral lines with similar spectra taken in the laboratory. If the universe were static as Einstein originally thought, the galactic and laboratory spectra would have been identical. What Hubble found surprised him and everyone else. The light from every distant galaxy was distinctly on the red side. No doubt about it, Hubble knew that they were all moving away from us. Some galaxies were moving slowly, and some were racing away, but except for a few very nearby galaxies, they were all outward bound. This must have puzzled Hubble. It meant that in the future the galaxies would spread out to ever-farther distances. Even more bizarre, it meant that in the past the galaxies were closer to us, at some point maybe even on top of us!

Hubble was also able to make a rough determination of the distances to the various galaxies, and he found a pattern: the more distant the galaxy, the faster its recessional velocity. The closer galaxies were hardly moving, but the most distant ones were speeding away with tremendous velocities. On a piece of graph paper, Hubble made two axes: on the horizontal axis he plotted the distance to each galaxy; on the vertical axis, its velocity. Each galaxy was plotted as a single point on the graph. What he found was extraordinary; most of the points fell on or near a straight line.

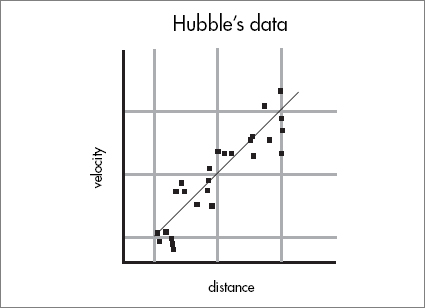
This meant that the recessional velocity not only increased with distance but was directly proportional to the distance. One galaxy, twice as far as another, appeared to recede twice as fast. This was a new, totally unexpected, regularity in the universe: a new cosmological law, Hubble’s Law.
Galaxies are receding away from us with velocity proportional to their distance.
An even more precise formulation is:
galaxies are receding away from us with velocity equal to the product of their distance and a numerical parameter called the Hubble constant.
³

Well, actually it wasn’t completely unexpected. Alexander Friedmann was a Russian mathematician who had studied Einstein’s theory of the universe, and in 1922 he published a paper claiming that Einstein might have been wrong in his 1917 paper. He argued that if the universe were not static, if it were changing as time evolved, then the cosmological constant would be superfluous. The Friedmann universe was, like Einstein’s, a closed-and-bounded 3-sphere. But unlike Einstein’s, Friedmann’s universe grew with time. If Einstein’s universe was like a static balloon, Friedmann’s was like the surface of an expanding balloon. Get yourself a balloon and mark its surface with dots to represent the galaxies. Sprinkle them more or less uniformly. Then slowly blow it up. As the balloon expands, the dots get farther apart, every dot receding from every other dot. No dot is special, but each sees all the others moving away. This was the essence of Friedmann’s mathematical universe.

What you may also notice if you are able to watch the dots is that the farther away they are from one another, the faster they separate. In fact the dots would do exactly what Hubble’s galaxies did. Hubble’s Law is the law of dots on the surface of an expanding balloon. Unfortunately Friedmann died in 1925, before he could learn of Hubble’s discovery or the fact that his—Friedmann’s—work had laid the foundation for all future cosmology.

Let’s review some of that cosmology.

“Only two things are infinite, the universe and human stupidity, and I’m not sure about the former.”

— ALBERT EINSTEIN

A couple of years ago I had the good fortune to be invited to South Africa in order to give some lectures in one of the universities. While I was there my wife and I made a trip to the Krueger National Park. The park is an enormous expanse of African veldt and home to all the large mammals of the continent. It was a fabulous experience. In the mornings and evenings we would go out in a Land Rover to view and photograph wildlife. We saw hippos, a rhino, Cape buffalo, a pride of lions devouring antelope, and most impressive of all, an angry rogue male elephant. But for me the most powerful sight of all was the southern sky on a dark, moonless night. The southern sky is much richer than the northern sky that I’m used to, and Krueger is almost completely free of light pollution. The sight of the Milky Way stretched clear across the sky is truly awe-inspiring. But the humbling sense of immensity is deceptive. The entire Milky Way together with all the visible stars is an infinitesimal corner of a much vaster space, homogeneously filled with a hundred billion galaxies, which can be seen only through a large telescope. And even that is a tiny portion of a much bigger cosmos.

According to my dictionary the word
homogeneous
means “uniform in structure or composition throughout.” When applied to oatmeal it means nice and smooth, i.e., without lumps. Of course if you look at the oatmeal with a magnifying glass, it hardly looks homogeneous. The point is that when you say something is homogeneous, you must qualify the statement by adding “on scales larger than some specified size.” Well-stirred oatmeal is homogeneous on scales larger than an eighth of an inch. Farmer Brown’s wheat field in the middle of Kansas is homogeneous on scales larger than a few feet.

Well, not quite. The oatmeal is only homogeneous on scales from an eighth of an inch to the size of the bowl. Farmer Brown’s field is homogeneous on scales bigger than ten feet but smaller than a mile. On scales of a mile or more, the countryside looks like a crazy quilt of rectangular fields. The right thing to say is that Farmer Brown’s field is homogeneous on scales between ten feet and a fraction of a mile.

Through the naked eye the African night sky is very
inhomogeneous.
The Milky Way is a bright, narrow band of light that divides a much darker background. But a look through a large telescope reveals billions of galaxies that are, on the whole, homogeneously distributed through the observable universe. According to astronomers the universe appears to be homogeneous and
isotropic
on scales larger than a hundred million light-years up to at least fifteen billion light-years. The fifteen billion light-year limit is certainly an underestimate that just represents our inability to see farther.