The Cosmic Landscape (18 page)

The anthropic controversy is about more than scientific facts and philosophical principles. It is about what constitutes good taste in science. And like all arguments about taste, it involves people’s esthetic sensibilities. The resistance to anthropic explanations of natural facts derives, in part, from the special esthetic criteria that have influenced all great theoretical physicists—Newton, Einstein, Dirac, Feynman—right down to the current generation. To understand the strong feelings involved, we must first comprehend the esthetic paradigm that is being challenged and threatened by dangerous new ideas.
Having spent a good part of a lifetime doing theoretical physics, I am personally convinced that it is the most beautiful and elegant of all the sciences. I’m pretty sure that my physicist friends all think the same. But most of us have no clear idea of what we mean by beauty in physics. When I have raised the question in the past, the answers varied. The most common was that the equations are elegant. A few answered that the actual physical phenomena are beautiful.
Physicists no doubt have esthetic criteria by which they judge theories. Conversations are peppered with words like
elegant, beautiful, simple, powerful, unique,
and so on. Probably no two people mean exactly the same thing by these words, but I think we can give broad definitions on which physicists will more or less agree.
If there is a difference between elegance and simplicity, it is too subtle for me. Mathematicians and engineers also use these terms more or less interchangeably, and they mean roughly the same thing as they do to physicists. An elegant solution to an engineering problem means one that uses the minimal amount of technology to accomplish the task at hand. Making one component serve two purposes is elegant. The minimal solution is the most elegant.
In the 1940s the cartoonist Rube Goldberg specialized in designing “Rube Goldberg machines,” which were fanciful, silly solutions to engineering problems. A Rube Goldberg alarm clock would have balls rolling down roller-coaster tracks, hammers tapping birds who pulled strings, and the whole thing ending with a bucket of water being poured on the sleeper. A Rube Goldberg machine was a decidedly inelegant solution to a problem.

Solutions to mathematical problems can similarly be evaluated in terms of elegance. A proof of a theorem should be as lean as possible, meaning that the number of assumptions, as well as the number of steps, should be kept to the minimum. A mathematical system such as Euclidean geometry should be based on the minimal number of axioms. Mathematicians love to streamline their arguments, sometimes to the point of incomprehensibility.
The theoretical physicist’s idea of elegance is fundamentally the same as the engineer’s or mathematician’s. The General Theory of Relativity is elegant because so much flows out of so little. Physicists also like their axioms simple and few in number. Any more than is absolutely essential is inelegant. An elegant theory should be expressible in terms of a small number of equations, each of which is simple to write. Long equations with too many symbols crowded together are a sign of an inelegant theory or perhaps a theory that is expressed in a clumsy way.
Where did this esthetic taste for simplicity come from?
1
It’s not just engineers, mathematicians, and physicists who derive a sense of satisfaction from a neat solution to a problem. My father was a plumber with a fifth-grade education. But he relished the symmetry and geometry of well-placed piping. He took deep professional pride in finding clever ways to minimize the pipe needed to run a water line from one point to another—without violating the esthetic rules of parallelism, rectangularity, and symmetry. It wasn’t because of the money he could save by cutting down on materials. That was trivial. His pleasure at an ingenious simplification and an elegant geometry was not so different from my own when I find a neat way to write an equation.
Uniqueness is another property that is especially highly valued by theoretical physicists. The best theories are ones that are unique in two senses. First of all, there should be no uncertainty about their consequences. The theory should predict all that is possible to predict and no more. But there is also a second kind of uniqueness that would be especially treasured in what Steven Weinberg calls a final theory. It is a kind of inevitability—a sense that the theory could not be any other way. The best theory would be not only a theory of everything, but it would be the
only
possible theory of everything.
The combination of elegance, uniqueness, and the power to answer all answerable questions is what makes a theory beautiful. But I think physicists would generally agree that no theory yet devised has fully lived up to these criteria. Indeed, there is no reason why any but the final theory of nature should be perfect in its beauty.
If you asked theoretical physicists to rank all theories esthetically, the clear winner would be the General Theory of Relativity. Einstein’s ideas were motivated by an elementary fact about gravity that every child can understand: the force of gravity feels the same as the force due to acceleration. Einstein performed a thought experiment in an imaginary elevator. His point of departure was the fact that in an elevator it is impossible to distinguish between the effects of a gravitational field and the effects of upward acceleration. Anyone who has been on a high-speed elevator knows that for the brief period of upward acceleration, you feel heavier: the pressure on the bottoms of your feet, the pull on your arms and shoulders feel exactly the same whether caused by gravity or the elevator’s increasing velocity. And during the deceleration you feel lighter. Einstein turned this trivial observation into one of the most far-reaching principles of physics: the principle of equivalence between gravity and acceleration, or more simply, the
equivalence principle.
From it he derived the rules that govern all phenomena in a gravitational field as well as the equations for the non-Euclidean geometry of space-time. It is all summarized in a few equations, the Einstein equations, with universal validity. I find that beautiful.
This brings up another facet of what beauty means to some physicists. It’s not just the final product of Einstein’s work on gravity that I find pleasing. For me a great deal of the beauty lies in the way he made the discovery: how it evolved from a thought experiment that even a child can understand. And yet I have heard physicists claim that if Einstein had not discovered the General Theory of Relativity, they or someone else would have soon discovered it in a more modern, more technical, but in my opinion, much less beautiful way. It’s interesting to compare the two routes to Einstein’s equations. According to these alternate-world historians, they would have attempted to build a theory along the lines of Maxwell’s electrodynamics. Maxwell’s theory consists of a set of eight equations whose solutions describe wavelike motions of the electromagnetic field. Those same equations also imply the ordinary forces between magnets and between electric charges. It is not the phenomena but the form of the equations that would have been the inspiration for modern-day theorists. The starting point would have been an equation for gravitational waves, similar in form to the equations describing light or sound waves.
2
Just as light is emitted from a vibrating charge, or sound from an oscillating tuning fork, waves of gravity are emitted by rapidly moving masses. While the equations describing the waves are mathematically consistent, trouble would arise when the waves were allowed to interact with massive objects. Inconsistencies would arise that do not occur in Maxwell’s theory. Undaunted, the theorists would have searched for extra terms to add to the equations to make them consistent. By trial and error they would find a series of successive approximations, each being better than the last. But at any given stage, the equations would still be inconsistent.
Consistency would be achieved only when an infinite number of terms were summed together. Moreover, when all the terms were added, the result would be exactly equivalent to Einstein’s equations! By a series of successive approximations, a route would have been found to a unique theory that would be equivalent to general relativity. There would be no need to ever think about accelerating elevators. The mathematical requirement of consistency, together with the method of successive approximations, would suffice. For some this is beautiful. It could hardly be called simple.
As for the elegance of the equations, I will display them in the wonderfully simple form that Einstein derived.
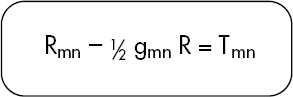
This small box with a few simply placed symbols contains the entire theory of gravitational phenomena: the falling of stones, the motion of the moon and earth, the formation of galaxies, the expansion of the universe, and much more.
The approach advocated by the modernists, although yielding the same content, would lead to an open-ended infinity of successive approximations. In that form the equations are distinctly inelegant.
Nevertheless, I have to admit that while the “modern derivation” may have missed the elegance of the Einstein equations, it did one thing rather well. It demonstrated the uniqueness of the theory. At each level of approximation, the extra terms needed to restore consistency are uniquely determined; the theory is unambiguous. Not only does it describe how gravity works, but it also shows that it could not have been otherwise.
The theory is also powerful. It can describe with great accuracy a very wide variety of gravitational phenomena from the earth’s ability to hold us to its surface to black holes at the center of quasars and gravitational waves from violent collisions of such black holes. With its elegant equations, an element of uniqueness, and the power to describe many phenomena, the General Theory of Relativity is the most beautiful physical theory yet devised. But as we have seen, it’s not only the content of a theory—what it says about the world—that makes it beautiful but also the form in which the equations are written and even the reasoning that went into its discovery.
If the physics beauty contest would be won by general relativity, the ugly-man prize would have to go to nuclear physics. The problem with nuclear physics is not that it leads to the ugliness of nuclear reactors and mushroom clouds. That’s technology, not physics. The problem is that the laws of nuclear physics are not clear or concise. As a result no elegant equations can capture its content, and no simple inevitable reasoning led to the discovery of its rules. If the rules simply declared that protons and neutrons attract each other according to some very simple force law, then the theory would be as elegant as atomic physics. But like the revisionist relativity, each approximation to the truth is defective. However, instead of appealing to mathematical consistency to improve it, various ad hoc rules of thumb must be introduced to make the theory agree with the properties of nuclei. Moreover, the rules of thumb that work for some nuclei don’t work for others. There is a boatload of different approximation schemes and successive trial-and-error strategies, but unlike the case of general relativity, it doesn’t add up to something simple, unique, and universally valid. Most theoretical physicists agree that the equations of nuclear physics are not in the least elegant, nor is their logic especially compelling.
Some physicists would claim that chemistry is ugly. Chemistry is also full of ad hoc recipes that have no universal validity. The first few lines of the periodic table are simple enough, but as you proceed down the table, more and more assumptions have to be added. The rules for molecular bonding are approximate and have plenty of exceptions. Sometimes they predict correctly and sometimes not. Whenever physicists want to disparage something as being unmotivated or overly complicated, they dismiss it as chemistry or even cookbook chemistry.
But a chemist might answer that physics is boring and impoverished. Chemistry is the subject that describes and explains the beauty and variety of the natural world. A flower, after all, is a collection of chemicals undergoing chemical reactions. To a scientific mind, understanding these processes adds to their esthetic value.
3
Many physicists and chemists look for beauty in the way in which very simple structures, like atoms, can combine themselves into macroscopic patterns. These phenomena, which are meaningful only for large numbers of atoms, are called
collective
or
emergent.
Phenomena that involve the collective behavior of many constituents
emerge
from the laws of simple elements such as atoms. Life is a collective phenomenon. So is the formation of a snowflake or the way atoms line up, side by side, to form a lovely crystal like a diamond. Yet another example is the cooperative behavior that allows many atoms to move without friction in a superconducting material. This is emergent beauty.