The Cosmic Landscape (16 page)

Whatever the number of fields, the principle is the same. Imagine a mathematical space with a direction for each field. If there are ten fields, then the space must be ten-dimensional. If there are one thousand fields, then the number of dimensions should be one thousand. This space is the Landscape. A point in the Landscape specifies a value for each field: a vacuum-weather condition. It also defines a particular set of elementary particles, their masses, and laws of interaction. If one could gradually move the universe from one point on the Landscape to another, all these things would gradually change. Responding to these changes, the properties of atoms and molecules would also change.

A map of real terrain would not be complete unless it indicated how the altitude varies from point to point. That’s the purpose of a topographical map, with its curved contours representing elevation. Even better than a topographical map would be a three-dimensional plaster model showing the mountains, valleys, and plains in miniature. Imagine we had such a model in front of us and add a little smooth ball, maybe a BB, to roll around on the model landscape. Place the ball anywhere and give it a little push: it will start to roll downhill until it eventually rolls to a stop at the bottom of some valley. Why does it do so? Many answers have been given to this question. The ancient Greeks believed that everything—every material—had its own place in the world and would always seek its correct level. I’m not sure what your answer would be, but as a physics professor, I would explain that the BB has potential energy, which depends on its elevation: the higher the altitude, the higher the potential energy. The BB rolls to a place of lowest energy or at least the lowest energy it can locate without having to climb over a hill to find an even lower valley. For a physicist studying the rolling BB, the contour map and the model landscape depict the variations of potential energy as the BB rolls along the landscape.

The Landscape of this book also has its highlands, lowlands, mountains, and valleys. It’s not little balls that roll around on it: whole pocket universes occupy locations on the Landscape! What do I mean when I say that a pocket universe occupies a place in the Landscape? It’s more or less the same as reporting the winter weather in Denver by saying that “the city occupies the point twenty-five on the thermometer scale.”

It sounds odd, but it makes perfect sense to say that the major cities of the world populate the thermometer and crawl about, on a daily basis or even from moment to moment.

But what is the meaning of the altitude of a point on the Landscape? Obviously it has nothing to do with elevation above sea level. But it does have to do with potential energy, not the energy of a BB, but the energy of a (pocket) universe.
⁶
And, as in the case of the BB, rolling toward the bottom of a valley represents the tendency of a universe to evolve toward lower potential energy. I will return to this point.

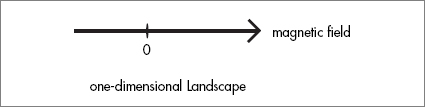
With this in mind let’s return to the Laws of Physics in the MRI machine. If the magnetic field were the only field, the Landscape would be one-dimensional, like the temperature scale, with the single axis labeling the strength of the magnetic field.

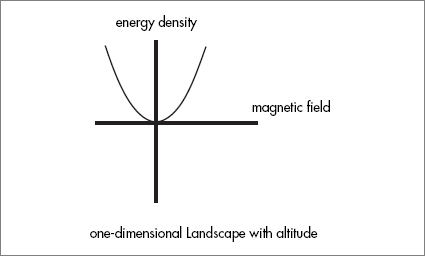
Magnetic fields do not come for free. It takes energy to create the field. In the early days of electromagnetic theory, before Michael Faraday introduced the field concept, it was thought that the energy was in the electric currents flowing through the wires of the electrical circuitry. But Faraday’s new vision of nature, in terms of fields filling space and affecting the behavior of charged objects, focused attention on the fields and away from wires, transformers, resistances, and other circuit elements. Physicists soon realized the great value of attributing energy to the field itself: wherever there is field, there is energy. The energy in the electromagnetic field of a beam of light will heat the cold object it illuminates.

There is also energy in the magnetic field of the MRI machine. Later we will encounter fields with vastly more energy content than the meager field in the MRI machine. The energy in the whole MRI field would be about enough to boil a few ounces of water.

Adding a vertical axis to the one-dimensional Landscape, we can plot the energy of every point. The energy contained in a magnetic field is proportional to the square of the field, which implies that the Landscape is a deep, parabolic valley with steep inclines on either side.

The magnetic field is only one of two fields that Faraday introduced, the electric field being the other. The electric field doesn’t affect a compass needle as a magnetic field would, but the electric field can make one’s hair stand on end. Strong electric fields deform atoms, pushing the negatively charged electrons in one direction and the positively charged nucleus in the other. The lopsided atoms can form long chains, positive nuclei adjacent to negative electron clouds (the group of atomic electrons bound to the nuclei), right down the line. If the electric field is strong enough, atoms will be torn apart. In such regions of the Landscape, atoms couldn’t exist at all. Neither, of course, could life.

Having both electric and magnetic fields adds diversity to the Landscape. It becomes two-dimensional. Since the electric field also has energy, the “altitude” varies in the two horizontal directions. This Landscape looks like a deep bowl surrounded by high, steep walls.

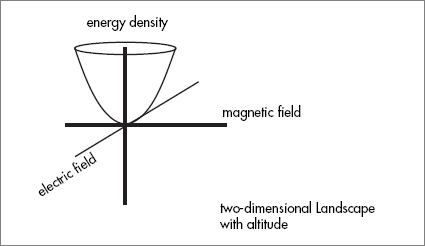
Because electric and magnetic fields affect the properties of electrons in different ways, there is greater potential for variety in the Laws of Physics. Electrons in the combined field move along more complicated trajectories than in the simpler pure magnetic field. Atomic energy levels show a greater degree of complexity, and the Landscape is more varied. If all space were uniformly filled with electric and magnetic fields, we could say that the Laws of Physics depend on where, in the two-dimensional Landscape, the universe is “located.” There are many more fields in nature than just the electric and magnetic fields, but the general principle is always the same. Every point on the Landscape—in other words, every value of the fields—has a corresponding value of energy density. If the fields are thought of as horizontal directions in the Landscape, one more vertical axis can be added to represent energy. If we call the vertical axis altitude, the Landscape can have plains, hills, mountain passes, and valleys.

Electric and magnetic fields are
vector fields,
which means that they not only have a size or magnitude at every point in space, but they also point in a direction. A compass located near a magnet points in the direction of the magnetic field. In a perfect world, the magnetic field would point precisely along the north-south axis everywhere on the surface of the earth. In the real world there are all sorts of variations from the ideal. A large iron deposit will influence the field in complicated ways. It’s exactly the ability to vary from point to point that makes magnetism a field.

The fields making up the Landscape are, for the most part, simpler than electric and magnetic fields. Most are
scalar fields.
A scalar is a quantity that has a size or magnitude but no direction. For example, temperature is a scalar. You won’t hear the weatherperson quote the temperature as “seventy-five degrees north by northwest.” Temperature has a magnitude but no direction. Air pressure and humidity are also scalars. But the weatherperson also reports a vector field: the wind velocity. Wind velocity is a perfect example of a vector field: it has magnitude and direction. Temperature, pressure, humidity, and wind velocity all share the property that they can vary from place to place. That’s what makes them fields. Of course they are just analogies. They have nothing to do with the fields that make up the Landscape.

The Higgs field is much like the magnetic field (except that it is scalar), but it is far more difficult to manipulate. It takes tremendous amounts of energy to change the Higgs field even a little bit. But if we could change it, the mass of each elementary particle (with the exception of the photon) would change.

Locomotives, cannon balls, and elementary particles all have mass. Mass is inertia; the more massive a body is, the harder it is to get it moving or to stop it. To determine the mass of an object, you subject it to a known force and measure its acceleration: the ratio of force to acceleration is its mass. If the object is at rest when the experiment begins, the measured mass is called the rest mass. In times past, a distinction was drawn between mass and rest mass, but today whenever the term
mass
is used it
always means rest mass.

It’s an empirical fact that all electrons have the same mass. So do all protons or any other type of particle. It’s because all electrons do have the same mass that we can speak of
the mass of the electron.
It’s the same for each kind of particle but, of course, the mass of one type of particle is not the same as another type. For example, the mass of the proton is about eighteen hundred times bigger than the electron mass.

Photons are eccentric oddballs when it comes to assigning them mass. The mass can’t be defined by accelerating them from
rest
because photons always move with the same velocity. Photons are particles of light, and as Einstein explained, light always moves at the speed of light. A photon can never be brought to rest; instead of slowing down, it would just disappear. Thus, the mass of a photon is zero. Any particle that travels with the speed of light is said to be
massless.

Of all the particles that are experimentally observed, only the photon is massless. But there is little doubt that at least one more massless particle exists. In the same way that an electron moving in an outer orbit of an atom radiates electromagnetic waves, a planet moving around the sun disturbs the gravitational field, thereby emitting gravitational waves. These gravitational waves are much too feeble to be detected on earth, but from time to time, tremendously violent events take place that produce very strong gravitational radiation. The collision of two black holes would release prodigious amounts of energy in the form of gravity waves that detectors on earth are being built to detect. Unless theoretical physicists are very badly mistaken, these waves will move with the speed of light. The reasonable presumption is that gravitational waves are made of massless quanta—gravitons.