The Cosmic Landscape (22 page)

Returning to my dictionary, I found the following definition for the term
isotropic:
“identical in all directions; invariant with respect to direction.” Isotropic is not the same as homogeneous. Here’s an example. Once while I was diving near a coral reef in the Red Sea, I saw a huge school of closely spaced, small, thin fish that filled quite a large volume homogeneously. For some strange reason, until I got too close, they all faced the same direction. The school appeared homogeneous over some range of scales, but definitely not isotropic. Every place within the school was like every other place, but every direction was not at all like every other direction. The direction the fish faced was special.

Cosmologists and astronomers almost always assume that the universe is homogeneous and isotropic; no matter where you are in the universe and which direction you are facing, you see the same thing. I don’t mean the nearby details but the overall, large-scale features of the universe. Cosmologists call this assumption the cosmological principle. Of course calling it a principle does not make it right. Originally it was just a guess, but gradually better and better observations of several kinds have convinced astronomers and cosmologists that the universe is indeed homogeneous and isotropic over scales ranging from a few hundred million light-years to at least a few tens of billions of light-years. Beyond that we don’t know for sure because there is a limit to our observations. It doesn’t matter how big our telescope, objects farther than fourteen billion light-years are impossible to observe. The reason is the simple fact that the universe is only about fourteen billion years old. In that time light could not have traveled more than fourteen billion light-years; light from more distant places just hasn’t reached us yet. In fact it’s a pretty safe bet that the universe is homogeneous and isotropic out to distance scales much larger than the observable part of the universe. But like Farmer Brown’s field, the universe may become a crazy quilt at a large enough distance: a patchwork of pocket universes.

For now, let’s adopt the very conventional point of view that the cosmological principle is correct out to the largest scales. This raises an interesting question: what kind of overall spatial geometry is compatible with the cosmological principle? By spatial geometry I mean the shape of space. Let’s begin with two-dimensional examples. A 2-sphere is a particular geometry. So are ellipsoids, pear shapes, and banana shapes.
⁴

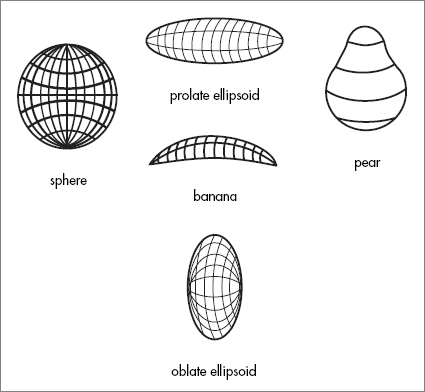
Among this list, only a sphere is homogeneous and isotropic. Like a circle, a sphere has perfect symmetry; every point is exactly like every other point. An ellipsoid, while not as symmetric as a sphere, still has a good deal of symmetry. For example, its mirror image looks just like itself. But not every place on the ellipsoid is the same as every other. The pear and banana are even less symmetric.

One way to describe the properties of a surface is by its curvature. The curvature of the sphere is absolutely uniform. Mathematically speaking it is a space of uniform positive curvature. The ellipsoid is also a positively curved space, but it is more curved in some places than others. For example, the prolate ellipsoid, which is shaped somewhat like a submarine, is curved more near its ends than at its waist. Of all these examples only the sphere is uniformly curved and homogeneous.

Spheres, ellipsoids, and the surfaces of fruits are closed-and-bounded geometries, meaning that they are finite in extent but without edges. But the truth is that no one knows if the universe is finite in extent. No cosmic Magellan has ever circumnavigated it. It’s entirely possible that the universe goes on forever, in which case it is unbounded, or infinite.

If we allow the possibility that the universe is infinite, then there are two more homogeneous, isotropic geometries. The first is obvious: the infinite flat plane. Think of it as a sheet of paper that goes on and on forever. There are no landmarks on the infinite plane to tell you where you are or which way you are facing. And unlike the surface of the sphere, the plane is not curved: mathematically it has zero curvature. Positive curvature for the sphere, zero curvature for the plane, and finally, the last homogeneous isotropic geometry, the negatively curved “hyperbolic geometry.” To help visualize this, think of a piece of duct pipe bent to a right angle. At the outer “elbow,” the sheet metal is positively curved like the sphere. The inner curved surface is the place where the curvature is negative.

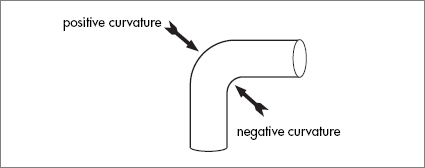
But of course the duct-pipe elbow is not homogeneous. The inner curved region is not at all the same as the outer positive curvature region. A better example is the surface of a saddle. Imagine continuing the saddle shape forever to form an unbounded negatively curved surface. It’s not easy to visualize, but it’s perfectly possible.

All three of these surfaces—sphere, plane, and hyperbolic geometry—are homogeneous. Moreover, all three of them have three-dimensional analogs: the 3-sphere, ordinary Euclidean three-dimensional space, and the most difficult to visualize, the hyperbolic three-dimensional space.

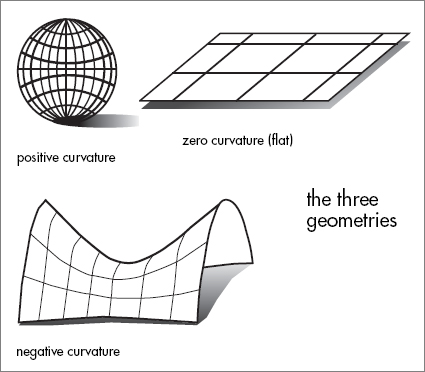
To envision the three standard types of cosmologies, think of each surface as a rubber sheet (or balloon in the case of the sphere) and fill the surface with dots to represent galaxies. Then start stretching the surface so that the dots begin to separate and the distance between any two grows with time. That’s all there is to it. You now have a rough idea of the three homogeneous, isotropic cosmologies. Cosmologists refer to these three cases as k = 1, k = 0, and k = -1. It’s just shorthand for positive curvature (the sphere), zero curvature (flat space or the plane), and negative curvature (hyperbolic space).

Is the universe finite and bounded as Einstein thought, or is it unbounded, filled with an endless infinity of stars and galaxies? The question fascinated cosmologists throughout the twentieth century and since, but the answer has proved elusive. In the rest of this chapter, I will tell you what has been discovered in the recent past and how it bears on the answer.

About a month ago I was home working on this book when I was disturbed by a knock on my front door. When I answered it, three very neatly dressed young people handed me a leaflet. I don’t usually bother arguing with proselytizers, but when I saw the title of the booklet—
Are You Prepared for the End of the Universe?
—I couldn’t resist asking them a few questions. When I asked them how they knew anything about the end of the universe, they told me that modern-day scientists had confirmed the biblical account of Armageddon and that the end of the universe was a scientific certainty.

They were probably right. Modern-day scientists do predict that the universe—at least the universe
as we know it
—will come to an end. Every reasonable cosmological theory says so. When and how it will happen varies from one set of assumptions to another, but all agree that it won’t happen for some tens of billions of years.

Broadly speaking there are two “end-of-the-world” scenarios. To understand them, think of a stone being thrown vertically into the air. Actually, I want to forget the air. Let’s throw the stone from an airless asteroid. One of two things can happen. The gravitational pull of the asteroid may be sufficient to pull the stone back, or it may not be. In the first case the stone will reverse its outward motion and come crashing back down, but in the second case it will overcome the gravitational attraction and fly off forever. It all depends on whether the initial velocity of the stone is faster than the
escape velocity.
The escape velocity depends on the mass of the asteroid: the bigger the mass, the larger the escape velocity.

According to the General Theory of Relativity, the fate of the universe is much like the fate of that stone.
⁵
The galaxies (and other material in the universe) have been shot out of the Big Bang explosion and are now flying away from each other. Meanwhile, gravity is working to pull them back. To put it another way, the balloonlike universe is growing, but gravitating matter is slowing down the expansion. Will the expansion keep going, or will gravity reverse it and eventually cause the universe to start shrinking? The answer is quite similar to the case of the asteroid and the stone. If there is enough mass in the universe, it will reverse direction and eventually collapse in a dreadful, big, superheated crunch. On the other hand, if there is not enough mass, the universe will keep expanding indefinitely. In this case the end may be gentler, but eventually the universe will become so thinned out that it will die a cold death.

For both the stone and the universe there is a third possibility. The stone might be precisely at the escape velocity. This would require a perfect balance between gravitational attraction and outward velocity. If you do the math in this case, you will find that the stone keeps going but at an ever-decreasing velocity. The same is true of the universe. If there is an exact balance between mass density and outward expansion, the universe will eternally expand but at an ever-decreasing rate.

Three possible geometries and three possible fates; is there a connection? Indeed there is. Einstein’s theory of gravity (without a cosmological constant) relates geometry to the presence of mass; mass affects geometry. The Newtonian dictum that “mass is the source of the gravitational field” is replaced by “mass warps and bends space.” That’s the link that relates the three geometries to the three fates. The details are in the difficult mathematics (tensor calculus and Riemannian geometry) of general relativity, but the result (with no cosmological constant) is easy to understand:

1. If the mass density in the universe is large enough to reverse the outgoing expansion, it will distort space into a sphere, a 3-sphere that is. This is the case of a closed-and-bounded universe. And its fate is a final crunch or, in the technical jargon, a
   singularity.
   This case is called the
   closed universe,
   or the k = 1 universe.
   
2. If the mass density is less than the minimum amount needed to close the universe, then it is also insufficient to reverse the motion. In this case it distorts space into a hyperbolic geometry. The hyperbolic universe expands forever. It’s called the
   open universe,
   or the k = –1 case.
   
3. If the universe is right on the knife-edge, between open and closed, then the geometry of space is flat, uncurved, Euclidean space, but the universe endlessly expands, albeit at an ever-diminishing rate. This is called the flat universe, and it is labeled k = 0.
   

So, which is it?

Some say the world will end in fire,

Some say in ice.

From what I’ve tasted of desire

I hold with those who favor fire.

But if it had to perish twice,

I think I know enough of hate

To know that for destruction ice

Is also great

And would suffice.

— Robert Frost,
“Fire and Ice”

When I asked the three young missionaries if it would be the hot death or the cold death, they said that it all depended on me. Very probably it would be the hot death unless I changed my ways.