The Cosmic Landscape (23 page)

Physicists and cosmologists are less certain of the final reckoning. For decades they have tried to determine which of the three fates will rule the last days. The first way to find out is very direct: use telescopes to look out into the distant reaches of space and count all the mass that can be seen—stars, galaxies, giant clouds of dust, and everything else that can be seen or deduced. Is the gravitational pull of all that material enough to turn the expansion around?

We know how fast the universe is expanding today. Hubble determined that the velocity of a distant galaxy is proportional to its distance—the factor of proportionality being the Hubble constant. This quantity is the best measure of the expansion rate: the larger the Hubble constant, the faster every galaxy is moving away from us. The units of the Hubble constant are velocity per unit distance. Astronomers usually quote it as “kilometers per second per megaparsec.” Everyone will recognize kilometers per second as a unit of velocity. One kilometer per second is about three times the speed of sound, i.e., Mach 3. The megaparsec is less familiar. It’s a unit of length, convenient for the study of cosmology. One megaparsec is about three million light-years, or thirty million trillion kilometers, a little more than the distance to our neighboring galaxy, Andromeda.

The value of the Hubble constant has been repeatedly measured over the years and has been the subject of a lively debate. Astronomers agreed it was somewhere between fifty and one hundred kilometers per second per megaparsec, but only in the recent past has the answer been resolved as about seventy-five in these units. The implication is that at a distance of one megaparsec, the galaxies are receding with a velocity of 75 km/ sec. At two megaparsecs their velocity is 150 km/ sec.

Now 75 km/ sec sounds awfully fast by terrestrial standards. At that rate it would take about ten minutes to circumnavigate the earth. But it’s not at all fast from the viewpoint of a physicist or astronomer. For example, the pinwheel motion of the Milky Way imparts a velocity to the earth that’s ten times faster. And by comparison with the speed of light, it’s a snail’s pace.

In fact, according to Hubble’s Law, the Andromeda Galaxy should be receding from us at about 50 km/ sec—but in reality it is moving toward us. It is so close that the Hubble expansion is counteracted by the gravitational pull of our galaxy. However, Hubble’s Law was never intended to be exact for a galaxy as close as Andromeda. When we consider galaxies that are far enough apart to escape each other’s gravity, the law works very well.

Nevertheless, the expansion is slow, and it would take very little mass density to turn it around.

Knowing the expansion rate, it is a straightforward application of Einstein’s equations to compute how large a mass density would be required to prevent the universe from eternally growing. The answer? Just 10
^–25
kilograms per cubic meter would be the knife-edge value: just barely enough to eventually reverse the outward flow of the galaxies. That’s not much. It’s roughly the mass of fifty protons in a cubic meter. A tiny bit more would be enough to curve the universe into a 3-sphere and turn the Big Bang into a disastrous big crunch. If the density were exactly this critical value, the universe would be flat (i.e., k = 0).

Astronomers search the sky for matter in the form of stars, gas, and dust clouds: all the matter in the universe that emits or scatters light. Assuming that the universe is homogeneous, we can count up all the glowing mass in the general vicinity of our galaxy and measure the average cosmic mass density. The number is remarkably small, only one proton mass per cubic meter: too small by a factor of fifty to close the universe. The obvious implication is that we are living in an infinite open (k = –1) universe with negative curvature and that it will go on expanding forever.

But astronomers and cosmologists have always been wary of jumping to this conclusion. Unlike physics, where being wrong by a factor of fifty is a disgrace, astronomy, until very recently, was a crude science. Estimates could easily be off in either direction by factors of ten or one hundred. Given that the mass density might have had any value, the fact that it came out so close to the critical density filled cosmologists with suspicion. And they were right to be suspicious.

There is another way to determine the mass of a galaxy besides just measuring the light from it, a much more direct and reliable way. And that’s to use Newton’s laws. Let’s return to the asteroid and the stone. Now, instead of moving vertically, the stone is moving in a circular orbit around the asteroid. The gravity of the asteroid keeps the stone in orbit. The key observation, which goes back to Newton, is that by measuring the velocity of the stone and the radius of its orbit, you can determine the mass of the asteroid. In a similar fashion, by measuring the velocity of stars in the outermost parts of a rotating galaxy, astronomers can measure the galaxy’s mass. And what do they find?

The galaxies are all heavier than the astronomers had thought. Roughly speaking, every galaxy is about ten times more massive than all the visible stars and interstellar gas that it contains. The remaining nine-tenths of the mass is a mystery. It is almost certainly not made of the things that comprise ordinary matter: protons, neutrons, and electrons. Cosmologists call it dark matter: dark because it gives off no light.
⁶
Nor does this ghostly matter scatter light or allow itself to be visible in any form, except through its gravity. So strange is modern science. For all these years—since the time of John Dalton—all matter was thought to be the usual stuff of chemistry. But now it seems that 90 percent of all the matter in the universe is something we know nothing about.

As astronomers were in the slow process of convincing themselves that dark matter is really there, theoretical physicists were busy postulating all sorts of new elementary particles for all kinds of reasons. Neutrinos were a very early example, superpartners were another, but they certainly don’t exhaust the imaginative list of hypothetical particles that were postulated for one reason or another. No one knows for sure what dark matter is, but the most likely solution is that there are new, heavy elementary particles that we haven’t discovered yet. Perhaps they are the nonidentical superpartner twins of ordinary particles—the bosonic partners of neutrinos or even the fermion partner of the photon. Perhaps they are a totally unsuspected class of elementary particles that no theorist has dreamed up yet. Whatever they are, they are heavy—they have mass and gravitate—but they have no electric charge to scatter or emit light. That’s all we really know. They must be all around us, constantly passing through the earth and even our bodies, but we can’t see them, feel them, or smell them. Without electric charge, they have no direct way of interacting with our senses. Very sensitive particle detectors are being built so that we may learn more about these mysterious objects, but for now it’s enough to know that they make galaxies ten times heavier than we thought.

The question of whether the universe is open and infinite or closed and finite has haunted astronomy for as long as there have been astronomers. A closed universe with a finite number of galaxies, stars, and planets is intuitively understandable, but an unbounded universe is almost incomprehensible. We have gotten closer to having enough matter to close the universe—tantalizingly close. Originally we were shy of the critical density by a factor of fifty. Now it is only a factor of five, but we are much more confident that we know the amount of mass that is out there. Could it be that the Hubble constant was not measured accurately? If it were smaller by a factor of two or three, then the mass density would be very close to closing the universe. So much hinges on getting this right that we want to close any possible loophole in the reasoning.

Astronomers have been closing in on the value of the Hubble constant for almost eighty years with ever more sophisticated instruments. It now seems very unlikely that it can be small enough to allow the universe to be closed. If this were the end of the story, then we would have to conclude that the cosmic mass density was insufficient to close the universe—but we’re not done yet.

The other way to determine if the universe is open, closed, or flat is very direct. Imagine a very large triangle in space, a triangle of cosmic proportions. To ensure that the sides are straight, we might take them to be the paths of light rays. A cosmic surveyor might measure the angles of the triangle, and if she were a student of Euclidean geometry, she might conclude that the sum of the angles should add up to 180 degrees—two right angles. The ancient Greeks were sure of it; they couldn’t conceive of space being any other way.

But modern geometers know that the answer depends on the geometry of space. If space is flat like Euclid thought, the sum of the three angles would add up to 180 degrees. On the other hand, if space is a sphere, the angles would add up to a total greater than 180 degrees. Less easy to visualize, the angles of a triangle in a negatively curved space will always sum to something less than 180 degrees.

Sending a team of cosmic surveyors billions of light-years to the corners of an immense triangle is not feasible, and even if it were, it would take billions of years to get there and billions of years more to get the result back to earth. But the ingenuity of astrophysicists is unbounded, and believe it or not, they devised a way to do the job without ever leaving the earth. I will return to how they did it after I explain the
cosmic microwave background,
or CMB. But the result is easy to state: space appears to be flat! The angles add up just as Euclid assumed. Or at least they add up to 180 degrees to within the accuracy of the experiment.

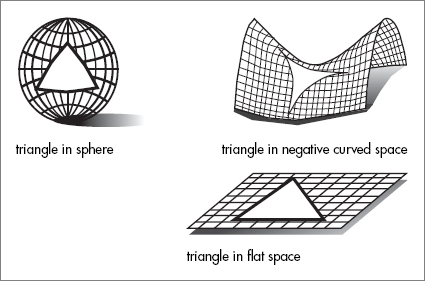
By now, dear reader, you must realize something is terribly wrong. We have two ways to determine if the universe is open, closed, or flat and two incompatible answers. The amount of mass in the universe appears to be five times too small to either close the universe or even to make it flat. But surveying cosmic triangles seems to leave little doubt that the geometry of the universe
is
flat.

Imagine a cosmic movie, a biography that follows the universe from its birth in fire to its present old age. But instead of viewing the movie in the ordinary way—from birth to old age—we run it backward, on rewind, so to speak. Instead of expanding, we see it contracting. The galaxies appear to move according to a reverse version of the Hubble Law—their velocity being proportional to their distance but approaching us instead of receding. Let’s follow one of those distant galaxies as it approaches us. Using Hubble’s Law (run backward), we can determine its velocity. Let’s say the galaxy is one megaparsec away. Hubble’s Law tells us that it is approaching with a velocity of seventy-five kilometers a second. Knowing how far away it is and how fast it is moving, it’s an easy exercise to determine how long it will be until the galaxy is on top of us. I will do it for you. The answer is about fifteen billion years. That’s the answer if we assume that the galaxy moves with a steady constant speed.

What if we started with a galaxy two megaparsecs away instead of one? Hubble’s Law tells us that it is moving twice as fast as the previous galaxy: twice as far but twice as fast. It too will arrive in our lap in fifteen billion years. In fact the same is true for any distant galaxy. According to this reckoning all the galaxies will merge into an undifferentiated mass in about fifteen billion years in the reverse movie.

But galaxies don’t move with uniform speed as they approach. In the forward version of the movie, gravity slows them as they recede. Thus, in the backward version, gravity speeds them up as they fall toward one another. This means that it should take less time for them to collide. When cosmologists carry out the correct calculation (in the forward version), they find that the galaxies were crowded together in a dense mass about ten billion years ago. This would mean that it has been only ten billion years since the hydrogen and helium gases began to differentiate themselves into the clumps that eventually became galaxies. To say it concisely, the universe, according to this reckoning, is ten billion years old.

Determining the age of the universe has been a bumpy ride. Originally Hubble underestimated the distances to the galaxies by about a factor of ten. This led him to conclude that the universe started its expansion a mere one billion years ago. But by Hubble’s time, rocks two billion years old had already been dated by their radioactivity. Obviously there was an error, and it was soon found. But a modern version of the problem still exists. Astronomers and astrophysicists, who study the detailed properties of stars in our galaxy, find that the oldest stars are older than the universe. They are about thirteen billion years old. The child is older than the parent!

In short, three big problems affect our thinking about the universe. First, there is the contradictory evidence concerning the geometry of space, whether it is open, closed, or flat. Second, is it really younger than the oldest stars? And third, the mother of all problems: is there a cosmological constant as Einstein originally believed, and if not, why not? Are these problems connected? Of course they are.