The Cosmic Landscape (44 page)

The D-brane is a model of a world with elementary particles behaving much like the real elementary particles. The only thing missing on the D-brane is gravity. That’s because the graviton is a closed string—a string with no ends. A string with no ends would not be stuck to the brane at all.

Could the real world (with the exception of the graviton) of electrons, photons, and all the other elementary particles—as well as atoms, molecules, people, stars, and galaxies—all take place on a brane? To the majority of theorists working on these problems, it seems the most likely possibility.

All kinds of things can be done with branes. Take a D2-brane—a membrane—and curve it into a 2-sphere. You’ve made a balloon. The trouble is that the tension of the membrane makes it quickly collapse like a punctured balloon. You could shape the D2-brane to form the surface of a torus, but this, too, would collapse.

But now imagine a brane that is stretched from one end of the universe to the other. The simplest example to visualize is an infinite D1-brane stretched right across the universe like an infinite cable. An infinite D-brane has no way to shrink and collapse. You can imagine that two cosmic giants hold its ends in place, but since the D-brane is infinite, the giants are infinitely far away.

There is no need to stop at D1-branes: an infinite sheet stretched across the universe is also stable. This time we would need many giants to hold the edges in place, but again, they would be infinitely far off. The infinite membrane would be a world with elementary particles that might resemble a “flatland” version of our own universe. You might think the creatures on the membrane would have no way of telling that more dimensions exist, but that would not be quite right. The giveaway would be the properties of the gravitational force. Remember that gravity is caused by gravitons jumping between objects. But gravitons are closed strings without ends. They have no reason to stick to the brane. Instead, they freely travel through all of space. They can still be exchanged between objects on the brane but only by traveling out into the extra dimensions, then back to the brane. Gravity would be like a science-fiction “message” telling the flatland creatures that there are more dimensions out there and that they are imprisoned on a two-dimensional surface.

The “unobserved” dimensions of gravity would in fact be easy to detect. When objects collide they can radiate gravitons, just as when electrons collide, they radiate photons. But typically the radiated gravitons will fly off into space and never return to the brane. Energy would be lost from the brane in this way. The flatland creatures would discover that energy doesn’t get converted to heat, potential energy, or chemical energy: it just disappears.

Now imagine that space has more dimensions than the usual three. Infinite D-3 branes could be stretched through space in the same way, and on a 3-brane all the usual things of our world could exist—except that gravity would be all wrong. The gravitational force law would reflect the fact that the graviton moves through more dimensions. Gravity would be “diluted” by spreading out in the extra dimensions. The result would be calamitous. Gravity would be much weaker, and galaxies, stars, and planets would be poorly held together. In fact gravity would be too weak to hold us to the earth even if the earth were somehow kept together.

Let’s take the extra dimensions—the ones that we can’t explore but the graviton can—and roll them up into a microscopically small compact space. The three dimensions of ordinary experience form an infinite room, but the other directions have walls, ceilings, and floors. The points on opposite walls or on ceiling and floor are matched just as I described in chapter 8.

To help visualize, let’s return to the example in which we compactified three-dimensional space by rolling up one direction. Beginning with an infinite room, each point of the ceiling was identified with the point on the floor directly beneath it. But now the floor has a carpet that stretches to infinity in infinite directions. The carpet is a D-brane. Imagine the carpet-brane slowly moving through the vertical dimension. It slowly rises from the floor like a magic carpet in the Arabian Nights. It continues to levitate and rise until it just touches the ceiling. And abracadabra—zap! The carpet instantly reappears at the floor.

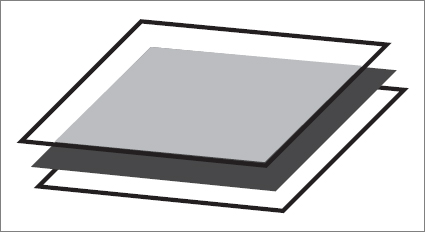
The graviton is still not attached to the carpet-brane, but now it can’t get very far away. There is very little room for it to move in the extra dimension. And if the extra dimension is microscopically small, then it is hard to tell if the graviton is off the brane. The result: gravity is almost exactly as it would be if, like everything else, the graviton moved on the brane. And of course there is nothing new if we replace the membrane with a D3-brane in a higher dimensional space. A D3-brane in the nine-dimensional space of String Theory would be very similar to our world if the extra six dimensions were tightly rolled up.

Most string theorists think we really do live on a brane-world, floating in a space with six extra dimensions. And perhaps there are other branes floating nearby, microscopically separated from us but invisible (to us) because our photons stick to our own brane, and theirs stick to their brane. Though invisible, these other branes would not be impossible to detect: gravity, formed of closed strings, would bridge the gap. But isn’t that exactly what dark matter is: invisible matter whose gravitational pull is felt by our own stars and galaxies? Polchinski’s D-branes open up all sorts of new directions. From our point of view, a universe with many brane-worlds living peacefully side by side is just one more possibility that can be found in the Landscape. Calabi Yau spaces of incredible complexity, hundreds of moduli, brane-worlds, fluxes (yet to come): the universe is starting to look like a world that only Rube Goldberg’s mother could love. To paraphrase the famous experimental physicist I. I. Rabi, “Who ordered all that stuff?”
¹

But by no means have we exhausted all the gimmicks and gadgets with which Rube can play. Here’s another: in addition to floating in the compact space, branes can also be wrapped around the compact directions. The simplest example is to go back to the infinite cylinder and wind a D1-brane around it. This would look the same as winding an ordinary string around the cylinder, except the string is replaced by a D1-brane. This object, from a distance, would look like a point particle on a one-dimensional line. On the other hand, suppose the compact space were an ordinary 2-sphere. You could try to wrap a string or D1-brane around the equator of the sphere like a belt around the middle of a fat man. But the belt could slip off the spherical fat man. A string or D1-brane wrapped on a sphere is not stable—it would not stay there for long. In the words of the physicist Sidney Coleman, “You can’t lasso a basketball.”

What about the torus—the surface of a bagel? Can a D1-brane be wrapped on the torus in a stable way? Yes, and in more ways than one. There are two ways to “belt the bagel.” One way is to run the belt through the hole. Try it. Take a bagel or donut and run a string through the hole. Wrap it around and tie it. The string can’t come off. Can you see the other way to belt the torus?

The deciding factor is the “topology” of the torus. Topology is the mathematical subject that distinguishes spheres from tori (plural of
torus
) and more complicated spaces. An interesting extension of the torus is a surface with two holes in it. Take a lump of clay and mold it into a ball. The surface is a sphere. Now poke a hole through it so that it resembles a donut: the surface is a torus. Next, poke a second hole. The surface is a two-holed generalization of a torus. There are more ways that you could wind a D1-brane on the two-hole torus than on the one-hole torus. A mathematician would call the sphere a
zero genus surface,
the torus a
genus one surface,
and the two-hole torus a
genus two surface.
Obviously you can poke any number of holes to make surfaces of any genus. The higher the genus, the more ways there are to wrap branes.

Having nine space dimensions, String Theory has six extra dimensions to hide by compactification. Six-dimensional spaces are vastly more complicated than two-dimensional spaces. Not only can you wrap D-1 branes but also there are higher dimensional versions of donut holes that allow you to wrap D2-, D3-, D4-, D5-, and D6-branes in hundreds of ways.

So far we have mainly thought about branes one at a time. But in fact you can have stacks of them. Think of the carpet in an infinite room. But why not have two carpets, one lying on top of the other? In fact it is possible to stack them up like stacks of carpets in a Persian bazaar. Just as the carpets could float freely of one another, a stack of D-branes can separate into several freely floating branes. But the D-branes are a bit like sticky carpets. If you bring them together, they will stick, forming a compound brane. This gives Rube Goldberg more options in designing his machine. He can place several carpet stacks at different heights in the room. He has new flexibility to make worlds with all sorts of properties. In fact with five carpets, stuck together in a stack of two and a stack of three, he can make a world with Laws of Physics that have many similarities to the Standard Model!

The locations of branes in the compact space are new variables to add to the moduli when counting the possibilities for creating a universe. From a distance, when the compact directions are microscopic—too small to see—the brane positions just appear to be additional scalar fields that define the Landscape.

Fluxes have emerged as one of the most important ingredients in the Landscape. They, more than anything else, make the Landscape prodigiously large. Fluxes are a bit more abstract, and harder to visualize, than branes. They are interesting new ingredients, but the bottom line is simple. From a distance they just look like even more scalar fields. The most familiar examples of fluxes are the electric and magnetic fields of Faraday and Maxwell. Faraday was not a mathematician, but he had a powerful ability to visualize. He must almost have been able to see the electromagnetic fields in his experimental apparatuses. His picture of the field of a magnet was
lines of force
emanating out of the North Pole and flowing back into the South Pole. At every point in space, the lines of force specify the direction of the magnetic field, while the density of the lines (how close together they are) specifies the field’s intensity.

Faraday pictured the electric field in the same way—lines flowing out of positive charges and into negative charges. Picture an imaginary sphere surrounding an isolated charged object with lines of electric force flowing out and receding off to infinity. The lines of force must pass through the sphere. These imaginary lines passing through the sphere are an example of the electric flux through a surface.

There is a measure of the total amount of flux passing through a surface. Faraday pictured it as the number of lines of force passing through the surface. Had he known calculus, he might have described it as a surface integral of the electric field. The idea of the
number of lines
was an even better one than Faraday knew. The flux through a surface happens to be one of those things that modern quantum mechanics tells us is quantized. Like photons, the unit of flux cannot be subdivided into fractions. Indeed, the flux cannot vary continuously but must be thought of in terms of discrete lines, so that the flux through any surface is an integer.

Ordinary electric and magnetic fields point along directions of three-dimensional space, but it is also possible to think of fluxes that point along the six compact directions of space. In a six-dimensional space the mathematics of fluxes is more complicated, but you can still think of lines or surfaces of force, winding their way over a Calabi Yau space, and passing through its donut holes.

To go more deeply into flux on a Calabi Yau space would require a good deal of modern geometry and topology. But the important conclusions are not so hard. As in the case of magnetic fields, the flux through the various donut holes is quantized. It is always an integer multiple of some basic flux unit. This means that to specify the flux completely all you need to specify is a number of integers—how many units of flux there are through each hole in the space.

How many integers are needed to describe the flux on a Calabi Yau space? The answer depends on the number of holes the surface has. Calabi Yau surfaces are far more complicated than a simple torus and typically have several hundred holes. Thus, hundreds of flux integers are part of the description of a point on the Landscape!

Thus far a typical setup can involve a few hundred moduli to fix the size and shape of the compact space, some branes located at various positions on the space, and now an additional few hundred flux integers. What more can we provide for Rube?

There are many more things to play with, but to keep this book of manageable size I will explain only one more—the conifold singularity. A soccer ball is a sphere. If you ignore the texture and seams on the surface, it is smooth. An American football, by contrast, is smooth everywhere except at the ends, where it comes to points. An infinitely sharp point somewhere on a smooth surface is an example of a
singularity.
In the case of the football, the singularities are called conical singularities. The pointy shape of the ends is like the tip of a cone.