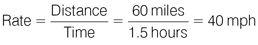How to Pass Numerical Reasoning (24 page)
Read How to Pass Numerical Reasoning Online
Authors: Heidi Smith

Rates conversion: practice drill 3: temperature
Q1
90°F
Q2
100°F
Q3
37°F
Q4
1,062°F
Q5
32°F
Q6
37°C
Q7
–15°C
Q8
–13°C
Q9
37°C
Q10
40°C
Rates practice questions answers
Q1
54 miles
Q2
21¾ miles
Q3
18 feet
Q4
7.2 miles
Q5
8 miles
Q6
7½ hours
Q7
1 hour 15 minutes
Q8
2 hours 30 minutes
Q9
40 minutes
Q10
1 hour 36 minutes
Q11
7
1
⁄
3
mph
Q12
1½ mph
Q13
10 mph
Q14
6,000 grains per minute
Q15
11 mph
Rates practice questions: explanations
Q1
Answer
= 54 miles
Estimate the answer
At 10 mph for 6 hours, he would cover 60 miles, so the total distance will be slightly less than 60 miles.
Calculate the answer
Apply the formula to find the distance:
Distance | = | Rate | × | Time |
Distance | = | 9 mph | × | 6 hours |
Distance | = | 54 miles |
Q2
Answer
= 21¾ miles
Estimate the answer
If she walked for 3 hours at 4 mph, she would complete 12 miles and would still have another 6 to walk. The total distance will be more than (12 + 6) miles = 18 miles as she is walking faster than 4 mph and for longer than 3 hours.
Calculate the answer
Apply the formula and plug in the numbers:
Distance | = | Rate | × | Time |
Distance | = | 4.5 mph | × | 3.5 hours |
Distance walked so far = 15.75 miles. |
She still has 6 miles to walk, so add this to the distance already covered = 21¾ miles.
Q3
Answer
= 18 feet
Estimate the answer
The singer shimmies 6 feet per minute while the bassist shuffles at half the speed, so he will cover 3 feet in a minute. In two minutes they will cover 2 × (6 feet + 3 feet) = 18 feet.
Calculate the answer
You can work out the rate for one of the two to traverse the whole stage by finding the average speed for both performers:
6 feet per minute + 3 feet per minute = 9 feet per minute
Now apply the formula to find the distance:
Distance | = | Rate | × | Time |
Distance | = | 9 feet per minute | × | 2 minutes |
The stage is 18 feet wide.
Q4
Answer
= 7.2 miles
Estimate the answer
The calculation is simple, so move straight on from the estimation.
Calculate the answer
In 1 second, the boat travels
1
⁄
1000
mile.
In 1 hour the boat travels:

In 2 hours the boat travels 2 × 3.6 miles = 7.2 miles.
Q5
Answer
= 8 miles
Calculate the answer
You can solve this problem with logic. Set up a diagram to help you to visualize the scenario.

Logic tells you that the return journey will take twice as long as the outbound journey because the pony is travelling at half the speed. In order to set up a ratio, you need to work out how much time each leg of the journey takes. You can set up an equation to help you to solve this. Let’s say the outbound journey from Hay to Oats takes M minutes. The return journey will take 2M minutes. Therefore, M + 2M = 2 hours or 3M = 120 minutes. To find M, divide by 3: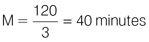
So the outbound journey (M minutes) takes 40 minutes and the return journey (2M minutes) takes 80 minutes (or 2 hours – 40 minutes = 80 minutes). Now you can plug in the numbers to the relevant formulae:
Distance | = | Time | × | Rate |
Distance | = | 40 minutes | × | 12 mph |
Distance | = | 2 | × | 12 mph |
The distance between the hay and the oats is 8 miles.
Q6
Answer
= 7½ hours
Estimate the answer
As we do not know the distance of the restricted stretches of railway, we have to assume that the restriction could apply to the whole journey. If the train travels at 50 per cent of 100 mph, it travels at 50 mph for 375 miles. 375 ÷ 50 = approximately 7, so you are looking for an answer of a little more than 7 hours.
Calculate the answer
Apply the formula for Time and plug in the numbers:
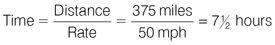
The minimum time the traveller must allow is 7½ hours.
Q7
Answer
= 1¼ hours
Estimate the answer
In one hour, 4 gallons × 60 minutes water will be discharged, which is 240 gallons. Therefore your answer will be at least one hour and less than two.
Calculate the answer
You are looking for the time required to fill the paddling pool, so set up the formula for Time.
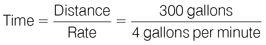
It takes 75 minutes to fill the paddling pool, but the question asks for the answer in hours, so convert from minutes to hours by dividing by 60: 75 ÷ 60 = 1.25 hours.
Q8 8
Answer
= 2 hours 30 minutes
Estimate the answer
If Mike drove home at the same speed, the total driving time would be 2 × 90 minutes = 180 minutes or 3 hours. If Mike drove twice as fast on the way home, the return journey would take him 45 minutes, or half the time of the outward journey. The total time would be 1½ hours + 45 minutes = 2 hours and 15 minutes. Your answer will therefore be between 2 hours and 15 minutes and 3 hours.
Calculate the answer
You may find it helpful to sketch a diagram to help you visualize the problem.

Pick numbers to help you to answer this question. Let’s assume that the distance driven is 60 miles. Apply the formula to find the rate: