How to Pass Numerical Reasoning (25 page)
Read How to Pass Numerical Reasoning Online
Authors: Heidi Smith

If he drives one and a half times faster on the way home, he drives at 1.5 × 40 mph = 60 mph. So on the return journey he drives 60 miles at 60 mph and the journey takes 1 hour. The total time is therefore 1 hour 30 minutes + 1 hour = 2 hours and 30 minutes.
Q9
Answer
= 40 minutes
Estimate the answer
You may find it helpful to set up a rough diagram to help you visualize what is going on in the question:
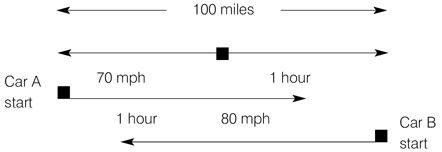
You will see that within an hour, both cars will have travelled more than halfway, and therefore they will have met within 1 hour.
Calculate the answer
If Car A remained stationary and Car B travelled at the combined speeds of Car A and Car B, the meeting point would be the same as if both cars travelled towards each other, setting off at the same time. The combined speed of Car A and Car B = 70 + 80 = 150 mph. Set up the relevant formula to find the time.
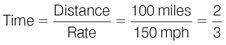
2
⁄
3
hour = 40 minutes. The cars will meet after 40 minutes.
Q10
Answer
= 1 hour 36 minutes
Estimate the answer
As the small car is travelling almost as fast as the large car, the small car will arrive later than 8 hours after the start of the journey.
Calculate the answer
In order to find the average speed of the small car, find the average speed of the family car first. Apply the formula to find the rate and plug in the numbers.
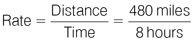
The family car travels at an average speed of 60 mph. The small car travels at
5
⁄
6
the speed of the family car:
5
⁄
6
× 60 mph = 50 mph. Now apply the formula to find time: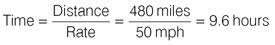
The small car arrives after 9.6 hours. The family car journey takes 8 hours and the small car journey takes 9.6 hours, so the small car arrives 1 hour and 36 minutes after the family car.
Q11
Answer
= 7
⁄
mph
Estimate the answer
If Jenny took 4 hours to complete four circuits, you would know that her average speed is 5.5 mph. Since she completes four circuits in less time, her average speed will be slightly faster than 5.5 mph.
Calculate the answer
Find the total distance Jenny runs in four laps of the park: 4 × 5.5 = 22 miles. Now apply the formula to find the rate:
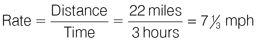
Jenny’s average speed is 7
1
⁄
3
mph.
Q12
Answer
= 1½ mph
Estimate the answer
The calculation is simple so move straight on and work out the answer.
Calculate the answer
If Jake managed to pedal for another 30 minutes at the same speed, he would pedal 2 × ¾ mile = 1½ miles. His speed is therefore 1½ miles per hour.
Q13
Answer
= 10 mph
Estimate the answer
The calculation is simple so move straight on and work out the answer.
Calculate the answer
Apply the formula to find the average of two rates and plug in the numbers:

Q14
Answer
= 6000 grains per minute
Estimate the answer
A quick conversion tells you that 2 minutes and 24 seconds = 144 seconds. If 14,400 grains of sand pass through the timer in 144 seconds, then 14,400/144 grains of sand will pass through every second.
Calculate the answer
Set up a proportion to find the fraction of the sand that has passed through the timer after 2 minutes and 24 seconds. This will allow you to find the total time required for 18,000 grains of sand to pass through.
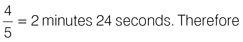


Now you can set up the formula to find the rate and plug in the numbers:

Answer
= 6,000 grains per minute.
Q15 5
Answer
= 11 mph
Estimate the answer