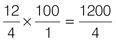How to Pass Numerical Reasoning (26 page)
Read How to Pass Numerical Reasoning Online
Authors: Heidi Smith

As there are three different speeds to calculate, work out each one separately.
Calculate the answer
Remember that you cannot simply add the rates together and find the average. First convert the time to the lowest unit (ie minutes): Swim = 48, Cycle = 299, Run = 403:
total = 750 minutes = 12.5 hours.
Now apply the formula to find the average rate and plug in the numbers.
140.6 ÷ 12.5 = 11.248. The question asks for the answer to the nearest mile, so the answer is 11 mph.

Work rates answers
Q1
1 hour 12 minutes
Q2
10 minutes
Q3
18 minutes
Work rates practice questions explanations
Q1
Answer
= 1 hour and 12 minutes
Apply the formula and plug in the numbers.
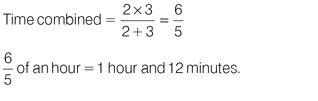
Q2
Answer
= 10 minutes
Apply the formula, plug in the numbers and work through the method.
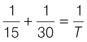
Find the lowest common denominator:
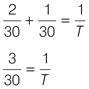
Reduce to its lowest terms.
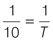
Find the reciprocal by inverting the fraction.
T
= 10 minutes.
Q3
Answer
= 18 minutes
First work out how long it will take both computers working together to complete all the tasks by applying the formula and plugging in the numbers.
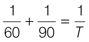
Find the lowest common denominator and add the fractions:
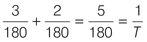
Reduce the fraction to its lowest terms:
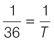
Find the reciprocal or
T
by inverting the fraction.
T
= 36 minutes. If it takes 36 minutes to complete a set of tasks, it will take 18 minutes to complete half the set.
• Terms used in this chapter
• Converting between percentages, fractions and decimals
• Converter tables
• Working with percentages
• Simple interest and compound interest
• Answers to
Chapter 4
Percentage
: One part in every hundred.
A percentage is a special type of ratio, which compares a number to 100. ‘Per cent’ or the ‘%’ sign mean ‘out of 100’. Expressed as a fraction, 1 per cent is expressed as 1 out of 100, or
1
⁄
100
, and is the mathematical relationship used most commonly in everyday life. For example, we are used to hearing that our local supermarket has a 10 per cent weekend sale, or that interest rates will change by ¼ per cent, or that inflation has risen by 5 per cent on last year’s index. The key to understanding problems involving percentages is to ask yourself first what the problem is about, then to decide whether you have enough information to answer the question. This chapter will guide you through the concepts and formulae to help you tackle percentage problems.
Test-writers love percentages! In most aptitude tests you will have to work out percentages, so it is worth understanding how they work. Practise as much as you can, so that you start to recognize the kind of questions you may be asked. Many percentage questions require you to interpret data from tables, charts and graphs. This chapter provides a reminder of the background to percentages, and drills you in word problems involving percentages. In
Chapter 6
, you will have the opportunity to apply your knowledge of percentages to data presented in a variety of formats.
Converting between percentages, fractions and decimals
When you work with percentages, it is useful to know the decimal and fraction equivalents so that you have a number of tools at your disposal to help you arrive at the correct answer. This section shows you how to convert between percentages, fractions and decimals.
To express a fraction as a percentage
To express ½ as a percentage, multiply by 100:
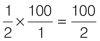
Reduce the fraction to its lowest terms:
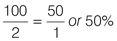
To express
12
⁄
4
as a percentage, multiply by 100: