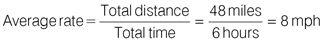How to Pass Numerical Reasoning (22 page)

Inbound journey:

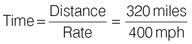
Reduce the fraction to its lowest terms:

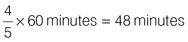
Total flying time for each pilot = 24 minutes + 48 minutes = 72 minutes. So the total time for both pilots is 144 minutes or 2 hours and 24 minutes.

Find the rate when you know the distance and time

Often, questions concerning rates relate to speed and you will need to apply this formula to find the answer to ‘find the speed’ type questions.

Worked example

Sanjay sets off walking to work at 7.10 am. He stops to buy a coffee and read his newspaper for 15 minutes and arrives at work at 8.55 am. The distance between his home and work is 6 miles. What is his average walking speed?

Estimate the answer

The actual walking time is 1 hour and 30 minutes and the total distance covered is 6 miles. If the time spent walking were 1 hour, the rate would be 6 mph. As the time taken to walk the distance is longer than 1 hour, the rate is slower. Your answer will therefore be less than 6 mph.

Calculate the answer

First convert the time to minutes. 1 hour 30 minutes = 90 minutes. Now apply the formula and plug in the numbers.

If Sanjay walks 1 mile in 15 minutes, he will walk 4 miles in 1 hour. The rate is therefore 4 mph.

Worked example: finding the average of two speeds

Jamie enters a biathlon, which requires her first to ride her bike between Thorpe Bay and Chalk Park and then to turn around and run back to Thorpe Bay on the same path. In this particular biathlon, Jamie cycles at a speed of 12 mph and runs at a speed of 6 mph. What is her average speed for the race?

Estimate the answer

When you combine average speeds, you cannot simply add the two together and then divide by 2, as you would do to find an average of two numbers. You can assume that the average speed will be closer to the lower of the two numbers (ie 6 mph) as more time will be spent on the leg of the journey that has the lower rate.

Calculate the answer

The formula to find the average rate of two (or more) rates is:

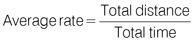
As you do not know the distance Jamie will travel, pick a distance that creates an easy calculation. For example, since 6 and 12 are both multiples of 24, you could choose 24 miles as the distance between the two points. (Equally, you could choose 12.) It may help you to draw a diagram to facilitate your thinking.

First work out the time it takes Jamie to complete each leg of the journey by plugging in the numbers to the relevant formula. In this instance, use:

Outbound time: Thorpe Bay to Chalk Park:

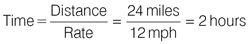
Inbound time: Chalk Park to Thorpe Bay:

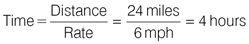
So it takes Jamie (2 + 4) hours to complete the whole distance of 48 miles. Now apply the formula to find the average rate.