How to Pass Numerical Reasoning (39 page)
Read How to Pass Numerical Reasoning Online
Authors: Heidi Smith

Take your cue from the question and plug in the numbers to the formula:

Remember the colon represents ‘to’ so plug in the answer 32 : 1.
Q2
Answer
= 1 : 2
Games Lost = 9
Games Won = 18
Ratio of Lost : Won = 9 : 18
Divide both sides by 9 to reduce the ratio to its simplest form: Lost to Won = 1 : 2.
Q3
Answer
= 16 : 9
Convert the units to the smaller of the two units: 1 hour 20 minutes = 80 minutes.
Potato : Pie = 80 : 45
Divide both sides by 5 to reduce the ratio to its simplest form: Potato : Pie = 16 : 9.
Q4
Answer
= 5 : 6
Week 2 = 250 miles
Week 3 = (250 + 50) miles
Week 2 : Week 3 = 250 : 300
Divide both sides by 50 to reduce the ratio to its simplest terms: Week 2 : Week 3 = 5 : 6.
Q5
Answer
= 3 : 2
Convert the weights to the smaller unit.
Currants = 1 lb 2oz = 18 oz
Currants : Sultanas = 18 : 12
Divide both sides by 6 to reduce the ratio to its simplest form: Currants : Sultanas = 3 : 2.
Q6
Answer
= 8 : 11
You are given a ‘part to part’ ratio and asked to find a ‘part to whole’ ratio. ‘All instruments’ is the parent set and consists of two subsets: ‘stringed instruments’ and ‘non-stringed instruments’.
Part (strings) | + | Part (non-stringed instruments) | = | Whole |
8 | + | 3 | = | 11 |
Part (strings) to Whole (all instruments) ratio = 8 : 11. |
Q7
Answer
= 119 : 120
When a question asks you ‘what fraction of’, you are usually expected to find a part : whole ratio.
If 250 are left-handed, there are (30,000 – 250 = 29,750) right-handed people in the crowd.

Reduce the fraction to its lowest terms:
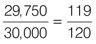
Now express the ratio in
x
: y format 119 : 120.
Q8
Answer
= 1: 3
You are being asked to find an unknown part in a part : part ratio. You know the actual values of the ‘part : whole’ ratio: Part (headstanders) to Whole (total in class) = 8 : 32.
Therefore Part (non-headstanders) to Whole (total in class) = (32 – 8) : 32.
Headstanders = 8 and Non-headstanders = 24, therefore Headstanders : Non-headstanders = 8 : 24.
Divide each part by 8 to express the ratio in its simplest terms = 1 : 3.
Q9
Answer
= 1: 2 : 5
Pick numbers to help you to solve this problem. You are given a part to part ratio of 3 : 5. From this you know that the ‘whole’ in the ‘part to whole’ ratio is (3 + 5) = 8. Pick a multiple of 8 to solve the problem, for example 24. So there are 24 diners in the restaurant and each part of the ratio represents (24 ÷ 8) = 3.
The actual values of vegetarians to meat-eaters = (3 × 3 parts) to (3 × 5 parts).
Ratio of vegetarians to meat-eaters = 9 : 15.
Of these 9 vegetarians,
2
⁄
3
eat fish.
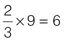
So 6 out of the 9 vegetarians eat fish and therefore the remaining 3 do not eat fish.
Ratio of vegetarians to vegetarian fish-eaters to meat-eaters = 3 : 6 : 15.
Divide each part by 3 to express the ratio in its simplest terms = 1 : 2 : 5.
Q10
Answer
= 17 : 28
You are asked to find a ‘part to whole’ ratio, where the ‘part’ is ‘tea’ and the ‘whole’ is ‘all drinks’.
First multiply the ratio of 1 to 6 by a factor which will allow you to divide easily by 3 and 4. By multiplying each part of the ‘part to part’ ratio (1 : 6) by 4, the result is 4 cups : 24 mugs. So there are part (4 cups) + part (24 mugs) = whole (28 drinks).
You know that ¼ of the cups are filled with tea:
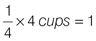
You also know that
2
⁄
3
of the mugs are filled with tea: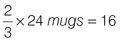
So there are 17 tea drinks on the table out of a possible 28 drinks. So the ratio of tea to all drinks = 17 : 28.
Q11
Answer
= 1375 miles
If ½ cm = 250 miles, 1 cm = 500 miles.
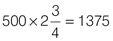
Q12
Answer
= £180
Anne’s 5 parts equal £225. 1 part is therefore £225 ÷ 5 = £45. Paula therefore receives 4 × £45 = £180.
Q13
Answer
= 15 games
The ratio of games won to games lost:
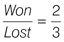
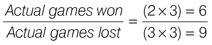
Total games = 6 + 9 = 15 games.
Q14
Answer
= 2 hours
If Charlotte ran the first half of the marathon in
4
⁄
5
(time) of the second half, then the second half took her
5
⁄
5
(time) of the second half. The total time is therefore: