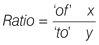How to Pass Numerical Reasoning (34 page)
Read How to Pass Numerical Reasoning Online
Authors: Heidi Smith

Now multiply both sides by the reciprocal of
2
⁄
3
× O: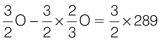
Now simplify the equation:
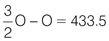
Multiply both sides by 2:
O = 2 × 433.5 = 867
Alternatively, use logic to approximate the answer. If 289 = 33.3%, then 3 × 289 = 100%.
Q9
Answer
= £61.86
The first 21 books cost £6 each = 21 × £6 = £126.
The next 9 books are discounted by 4% on the wholesale price of £6:
Number of books | × | (Original price 4% discount) | = | Discounted price |
9 books | × | (£6 × (1 – 0.04)) | = | £51.84 |
Total cost of wholesale order = (£126 + £51.84) = £177.84 The retail price of 30 books = £7.99 × 30 = £239.70 Retail price – Wholesale price = Amount saved £239.70 – £177.84 = £61.86 |
Q10
Answer
= 49 litres
The round trip of 248 miles requires (2 × 25 litres) = 50 litres. After the engine tune, fuel consumption is reduced by 2%. Decrease 50 litres by 2%: 50 × (1 – 0.02) = 49 litres
Simple and compound interest practice questions
Q1
£10,298.44
Q2
20%
Q3
5 years
Q4
Bank account
Q5
£418.25
Simple and compound interest practice questions explanations
Q1
Answer
= £10,298.44
Use the formula and plug in numbers:
Principal sum | × | Interest rate | × | Time period | = | Interest |
£9750 | × | 3.75% | × | 1½ years | = | Interest |
£9750 | × | 0.0375 | × | 1.5 | = | £548.44 (to nearest p) |
Total interest paid = £548.44. The question asks for the total amount in the account at the end of the term, so add the interest to the principal sum: £9750 + 548.44 = £10,298.44.
Q2
Answer
= 20%
First work out the actual amount of interest earned on the account:
Final sum | – | Principal sum | = | Total interest |
£2100 | – | £1500 | = | £600 |
Total time = 2 years. Plug in the numbers to the formula:

Q3
Answer
= 5 years
After 1 year, simple interest earned =
Principal sum × Interest (£60 × 1.25%)
£60 × 0.0125 = £0.75 per year simple interest.
Total interest earned during the term =
(Principal sum + interest) – Principal sum
£63.75 – £60 = £3.75
Divide the annual interest (£0.75) by the total interest (£3.75) to find the time period:
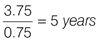
Q4
Answer
= bank account
Value of the house after 6 years = Principal sum × 40% increase
£40,000 × 1.4 = £56,000
Value of investment in the bank account =
Principal sum + (Principal sum × Interest × Time period)
£40,000 + (£40,000 × 0.09 × 6 years) = £61,600
The bank account investment yields an additional £5,600.
Q5
Answer
= £418.25
You can either use the formula to work out the amount of compound interest, or work out the total value of the certificate at the end of the period by working out the value of the certificate year on year
Year | Principal sum | × | Interest | = | Principal sum + Interest |
| | × | (1 + 2.8%) | | |
1 | £385 | × | 1.028 | = | £395.78 |
2 | £395.78 | × | 1.028 | = | £406.86 |
3 | £406.86 | × | 1.028 | = | £418.25 |
• Terms used in this chapter
• Working with ratios
• Ratios and common units of measure
• Types of ratio
• Using ratios to find actual quantities
• Proportions
• Answers to
Chapter 5
Proportion:
Equality of ratios between two pairs of quantities.
Ratio:
The comparison between two or more quantities.
When you define the relationship between two (or more) quantities of the same kind you are finding a
ratio
. A ratio tells you the relationship between quantities, but does not necessarily tell you the actual quantities. For example, the instruction ‘to bake a scone, use half the quantity of fat to one quantity of flour’ tells you the ratio of fat to flour, but does not tell you how much of each quantity to use. When you compare two ratios, you are finding a
proportion
. In this chapter you will learn first how to work with ratios, and then you will apply that knowledge to understand proportions and when to use them.
Ratios work in a similar way to fractions and are usually reduced to the lowest term. In aptitude tests, ratios are typically used to represent relative quantities of whole units, such as the ratio of adults to children in a playground, or the ratio of inches to miles on a map, or of gin to vermouth in a martini. You can set up a ratio in several different ways. For example, to define the relationship between 5 black cats and 10 white cats:
Method 1
Define the ratio in words, separating the quantities with ‘to’. For example:
The ratio of black cats to white cats is five ‘to’ ten.
Method 2
Separate the quantities with a colon, where the colon replaces the word ‘to’. For example:
The ratio of black cats to white cats is 5 : 10.
This can be reduced to its lowest terms like an equation. Simply divide both sides by the same number, so 5 : 10 = 1 : 2 when you divide both sides by 5.
Method 3
Write the ratio as a fraction in its lowest terms. For example:
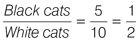
A simple way to remember which way to set up the fraction is with a formula: