How to Pass Numerical Reasoning (33 page)
Read How to Pass Numerical Reasoning Online
Authors: Heidi Smith

The question asks you to increase 4.5 by 9 = 4.5 + 9 = 13.5
Q2
Answer
= 33
⁄
%
Use the percentage increase formula:

New whole – original whole = actual amount of increase:
3200 – 2400 = 800
Plug in the numbers to the formula:

Reduce the fraction to its lowest terms:

Q3
Answer
= 23%
Let S represent the price of the stock.
Price of stock S following a 20% increase = S(1.2).
Price of stock S following a 20% and 2.5% increase = S(1.2) (1.025).
Final price = S(1.23).
1.23 represents a 23% increase.
Q4
Answer
= Year 3
This question requires you to work out the height of the tree each year as a percentage increase on the height of the previous year. To increase by 5%, multiply the whole by 1.05:
Year | Whole | × | 5% increase | = | New whole |
1 | 90 cm | × | 1.05 | = | 94.5 cm |
2 | 94.5 cm | × | 1.05 | = | 99.225 cm |
3 | 99.225 cm | × | 1.05 | = | 104.18625 cm |
Q5
Answer
= £28,222.50
Work out the percentage increase in salary between 2000 and 2001:
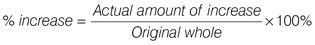
New whole – original whole = actual amount of increase:
£26,500 – £25,000 = £1,500
Plug in the numbers to the formula:
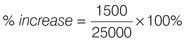
Reduce the fraction to its lowest terms:
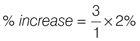
Percentage increase = 6%. Projected 2002 salary = £26,500 (6% + 0.5%)
£26,500 × (1 + 0.065) = £28,222.50
Q6
Answer
Pick numbers for this question and work through the question. Let P = 100.
First discount P by 25%:
100 × (1 – 0.25) = 75
The new price of P (=75) = 12.5% of Q:

Multiply by the reciprocal of the fraction to solve for Q:
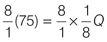
600 = Q and P = 100 and therefore:

Q7
Answer
= £85
A 15% discount is the same as saying that the bike will cost 85% of the original value (100% –15% = 85%). A further 20% discount is the same as 80% of the new value.
First discount the original price by 15%:
£125 × (1 – 0.15) = £106.25
Now discount the new whole (= £106.25) by a further 20%:
£106.25 × (1 – 0.2) = £85
Q8
Answer
= £867
Recall that 66
2
⁄
3
% = 2/3.
Sale price = 289; Original price = O. Now solve for O:
