Why Beauty is Truth (19 page)
Read Why Beauty is Truth Online
Authors: Ian Stewart

Harsh reality brought him down to earth. The resolvent equation for the quintic was not a quartic but an equation of
higher
degree, a sextic. The method that had simplified the cubic and quartic equations
complicated
the quintic.
Mathematics does not progress by replacing difficult problems by even harder ones. Lagrange's unified method failed on the quintic. Still, he had not proved the quintic to be unsolvable, because there might exist different methods.
Why not?
To Lagrange, this was a rhetorical question. But one of his successors took it seriously, and answered it.

His name was Paolo Ruffini, and when I say that he “answered” Lagrange's rhetorical question, I am cheating slightly. He
thought
he had answered it, and his contemporaries never found anything wrong with his answerâpartly because they never took his work seriously enough to
really try. Ruffini spent his life believing that he had proved the quintic unsolvable by radicals. Only after his death did it turn out that his proof had a significant gap. It was easily overlooked among his pages and pages of intricate calculations; it was an “obvious” assumption, one that he had never even noticed he was making.
As every professional mathematician knows from bitter experience, it is very difficult to notice that you are making an unstated assumption, precisely because it is unstated.
Ruffini was born in 1765, the son of a doctor. In 1783 he enrolled at the University of Modena, studying medicine, philosophy, literature, and mathematics. He learned geometry from Luigi Fantini and calculus from Paolo Cassiani. When Cassiani moved on to a post with the Este family, managing their vast estates, Ruffini, though still a student, took charge of Cassiani's analysis course. He obtained a degree in philosophy, medicine, and surgery in 1788, adding a mathematics degree in 1789. Soon afterward, he took over a professorship from Fantini, whose eyesight was failing.
Events interfered with his academic work. Napoleon Bonaparte defeated the armies of Austria and Sardinia in 1796, turned his sights towards Turin, and captured Milan. Soon he had occupied Modena, and Ruffini was forced to become involved in politics. He had planned to go back to the university in 1798, but refused, on religious grounds, to swear allegiance to the republic. The resulting lack of employment left him more time to carry out his researches, and he focused on the vexed question of the quintic.
Ruffini convinced himself that there was a good reason why no one had managed to find a solution: there wasn't one. Specifically, there was no formula involving nothing more esoteric than radicals that would solve the general quintic. In his two-volume tome
General Theory of Equations
, published in 1799, he claimed to be able to prove this, asserting, “The algebraic solution of general equations of degree greater than four is always impossible. Behold a very important theorem which I believe I am able to assert (if I do not err): to present the proof of it is the main reason for publishing this volume. The immortal Lagrange, with his sublime reflections, has provided the basis of my proof.”
The proof occupied more than 500 pages of largely unfamiliar mathematics. Other mathematicians found it somewhat daunting. Even today, no one is keen to wade through a very long and technical proof unless there is very good reason to do so. If Ruffini had announced a
solution
to
the quintic, his peers would surely have made the effort. But you can understand their reluctance to devote hundreds of hours to the claim of a negative result.
Especially when it might be wrong. Few things are more annoying than finding an error on page 499 of a 500-page mathematics book.
Ruffini sent Lagrange a copy in 1801, and after a few months' silence he sent another copy, with a note: “If I have erred in any proof, or if I have said something which I believed new, and which is in reality not new, finally if I have written a useless book, I pray you point it out to me sincerely.” Still no reply. He tried again in 1802. Nothing.
Several years passed without the recognition Ruffini felt was his due. Instead, vague rumors circulated, hinting that there were mistakes in his “proof,” but since no one said what those mistakes might be, Ruffini was unable to defend himself. Eventually, he decided, no doubt correctly, that his proof was too complicated, and set about finding something simpler. He achieved this in 1803, writing, “In the present memoir, I shall try to prove the same proposition with, I hope, less abstruse reasoning and with complete rigor.” The new proof fared no better. The world wasn't ready for Ruffini's insights or for the further proofs he published in 1808 and 1813. He never stopped trying to get his work recognized by the mathematical community. When Jean Delambre, who predicted the position of the planet Uranus, wrote a report on the state of mathematics since 1789, he included the sentence, “Ruffini proposes to prove that solving the quintic is impossible.” Ruffini promptly replied, “I not only proposed to prove, but in reality did prove.”
To be fair, a few mathematicians were happy with Ruffini's proof. Among them was Cauchy, who had a pretty poor track record when it came to giving credit where it was due, unless it was due to himself. In 1821, he wrote to Ruffini, “Your memoir on the general resolution of equations is a work which has always seemed to me worthy of the attention of mathematicians and which, in my judgment, proves completely the impossibility of solving algebraically equations of higher than the fourth degree.” But by then the praise was far too late.
Around 1800 Ruffini started teaching applied mathematics in the city's military school. He continued to practice medicine, looking after patients from the poorest to the richest in society. In 1814, after the fall of Napoleon, he became rector of the University of Modena. The political situation was still extremely complex, and despite his personal skills, the
great respect in which he was held, and his reputation for honesty, his time as rector must have been very difficult.
Simultaneously, Ruffini held the chairs of applied mathematics, practical medicine, and clinical medicine in the University of Modena. In 1817, there was a typhus epidemic and Ruffini continued to treat his patients until he caught the disease himself. He survived but never fully regained his health, and in 1819 he gave up his chair of clinical medicine. But he never gave up his scientific work, and in 1820 he published a scientific article on typhus based on his own experience as both physician and patient. He died in 1822, barely a year after Cauchy had written to praise his work on the quintic.

One reason Ruffini's work was not well received may have been its novelty. Like Lagrange, he based his investigations on the concept of a “permutation.” A permutation is a way to rearrange some ordered list. The most familiar example is shuffling a pack of cards. The usual aim here is to achieve some randomâthat is, unpredictableâorder. The number of different permutations of a pack of cards is huge, so the chance of predicting the outcome of random shuffling is negligible.
Permutations arise in the theory of equations because the roots of a given polynomial can be considered as a list. Some very basic features of equations are directly related to the effect of shuffling that list. The intuition is that the equation “does not know” the order in which you listed its roots, so permuting the roots should not make any important difference. In particular, the coefficients of the equation should be fully symmetric expressions in the rootsâexpressions that do not change when the roots are permuted.
But as Lagrange had appreciated, some expressions in the roots may be symmetric with respect to some permutations, but not others. These “partially symmetric” expressions are intimately associated with any formula for solving the equation. This feature of permutations was familiar to Ruffini's peers. Much less familiar was Ruffini's systematic use of another of Lagrange's ideas: that you can “multiply” two permutations to get another one by performing them in turn.
Consider the three symbols
a, b, c.
There are six permutations:
abc, acb, bac, bca, cab
, and
cba.
Take one of them, say
cba.
At first sight, this is just an ordered list formed from the three symbols. But we can also think of it
as a
rule
for rearranging the original list
abc.
In this case, the rule is “reverse the order.” And we can apply this rule not just to that list but to any list. Apply it to
bca
, say, and you get
acb.
So there is a sense in which
cba
Ã
bca
=
acb.
This idea, which is central to our story, probably makes more sense if we draw some diagrams. Here are two diagrams for the permutations that rearrange
abc
into
cba
and
bca:
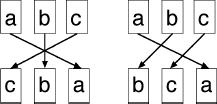
Two permutations of the symbols
a, b, c.
We can combine the two rearrangements into one, by stacking these pictures on top of each other. There are two ways to do this:
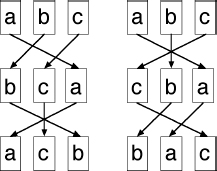
Multiplying permutations. The result depends on which comes first.
Now we can read off the result of “multiplying” the two permutations by writing down the bottom row, which here (left-hand picture) is
acb.
With this definition of “multiplication” (which is not the usual concept for multiplying numbers) we can make sense of the statement
cba
Ã
bca
=
acb.
The convention is that the first permutation in the product goes on
the
bottom
of the stack. It matters, because we get a different answer if we swap the two layers of the stack. The right-hand picture shows that when the permutations are multiplied in the opposite order, the result is
bca
Ã
cba
=
bac.